Question

【题目】综合与实践

在数学活动课上，老师给出如下问题，让同学们展开探究活动：

[问题情境]

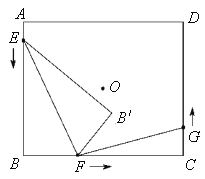
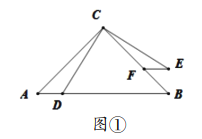
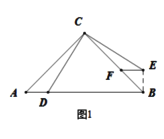
如图①，在中，，点为上一点，将线段绕点逆时针旋转，得到的对应线段为，过点作，交于点，请你根据上述条件，提出恰当的数学问题并解答．

　　　

[解决问题]

下面是学习小组提出的三个问题，请你解答这些问题：

（1）“兴趣”组提出的问题是：求证：；

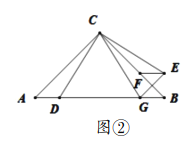
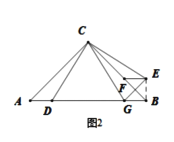
（2）“实践”小组提出的问题是：如图②，若将沿的垂直平分线对折，得到，连接，则线段与有怎样的数量关系？请说明理由；

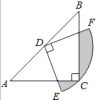
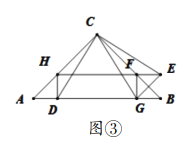
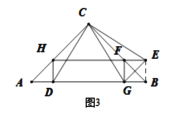
（3）“奋进”小组在“实践”小组探究的基础上，提出了如下问题：延长与交于点，连接，求证：四边形是矩形．

Answer 1

【答案】（1）见解析；（2），理由见解析；（3）见解析．

【解析】

（1）连接，证明，得到AD=BE，，证出∠ABE=90°，由平行线的性质得出∠FEB=90°，得出，证出EF=BE，即可得出结论；

（2）连接BE，由（1）可得出BE=BG=EF，证出，再由等腰直角三角形的性质即可得出结论；

（3）连接BE，证出CH=CF，证明，得出，证出，证明四边形为正方形，得出∠FGB=90°，因此，证明四边形是平行四边形即可得出它是矩形．

（1）证明：如图1所示：连接

，

在和中，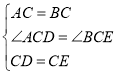

，

，

（2）解：

理由如下：如图2所示，连接.

由（1）可知，，

（3）证明：如图3所示，连接

，

，

，

与对称，点的对应点为，

，

在和中，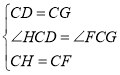

，

，

又，

，

由（1）、（2）可知，，

四边形为正方形，

，

，

，

又，

四边形是平行四边形，

四边形为矩形