题目内容
【题目】综合与探究:
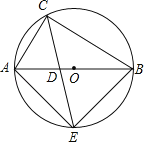
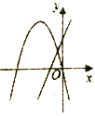
如图,已知在△ABC 中,AB=AC,∠BAC=90°,点 A 在 x 轴上,点 B 在 y 轴上,点![]() 在二次函数
在二次函数![]() 的图像上.
的图像上.
(1)求二次函数的表达式;
(2)求点 A,B 的坐标;
(3)把△ABC 沿 x 轴正方向平移, 当点 B 落在抛物线上时, 求△ABC 扫过区域的面积.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将点![]() 代入二次函数解析式即可;
代入二次函数解析式即可;
(2)过点![]() 作
作![]() 轴,证明
轴,证明![]() 即可得到
即可得到![]() 即可得出点 A,B 的坐标;
即可得出点 A,B 的坐标;
(3)设点![]() 的坐标为
的坐标为![]() ,解方程
,解方程![]() 得出四边形
得出四边形![]() 为平行四边形,求出AC,AB的值,通过
为平行四边形,求出AC,AB的值,通过![]() 扫过区域的面积=
扫过区域的面积=![]() 代入计算即可.
代入计算即可.
解:(1)∵点![]() 在二次函数的图象上,
在二次函数的图象上,
![]() .
.
解方程,得![]()
∴二次函数的表达式为![]() .
.
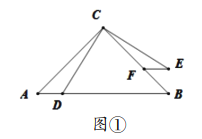
(2)如图1,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .
.

![]()
![]() .
.
![]() ,
,
![]()
![]() .
.
在![]() 和
和![]() 中,
中,
∵ ,
,
![]() .
.
∵点![]() 的坐标为
的坐标为![]() ,
,
![]() .
.
![]() .
.
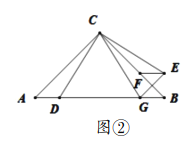
(3)如图2,把![]() 沿
沿![]() 轴正方向平移,
轴正方向平移,

当点![]() 落在抛物线上点
落在抛物线上点![]() 处时,设点
处时,设点![]() 的坐标为
的坐标为![]() .
.
解方程![]() 得:
得:![]() (舍去)或
(舍去)或![]()
由平移的性质知,![]() 且
且![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
![]()
![]() .
.
![]() 扫过区域的面积=
扫过区域的面积=![]() =
=![]()
![]() .
.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】某校号召全体学生1200人积极参加义工活动,小庆随机抽取部分学生一年中参加义工活动的次数情况进行统计,绘制了如下不完整的统计表和统计图.
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
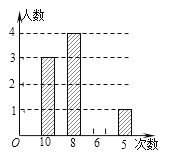
(1)表中数据![]() 为多少?并将条形统计图补充完整;
为多少?并将条形统计图补充完整;
(2)计算被抽取学生平均一年参加义工活动的次数;
(3)估计全校学生中参加义工活动8次的有多少人?