Question

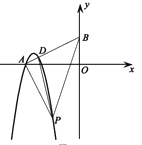
【题目】如图，正方形中，，E为的中点，将沿翻折得到，延长交于，，垂足为，连接．以下结论：平分；；；其中正确的个数是（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

由正方形的性质以及折叠的性质可得∠EBF=∠EFB，根据可得∠EBF=∠BFH，进而得出∠EFB=∠BFH，即可判断①，通过∠AED+∠FED=∠EBF+∠EFB得到∠AED=∠EBF=∠EFB=∠BFH即可判断②，通过折叠及正方形的性质得到Rt△DFG≌Rt△DCG（HL），设FG=CG=x，在Rt△BEG中运用勾股定理解出x，即可得到EG的长度，从而求出，即可判断③，由△FGH∽△EGB得到FH的长度即可判断④．

解：∵正方形中，AB=6，E为AB的中点，

∴AD=DC=BC=AB=6，AE=BE=3，∠A=∠C=∠ABC=90°，

∵△ADE沿DE翻折得到△FDE

∴∠AED=∠FED，AD=FD=6，AE=EF=3，∠A=∠DFE=90°，

∴BE=EF=3，∠DFG=∠C=90°

∴∠EBF=∠EFB，

又∵FH⊥BC，

∴FH∥AB

∴∠EBF=∠BFH

∴∠EFB=∠BFH

∴FB平分∠EFH，故①正确；

∵∠AED+∠FED=∠EBF+∠EFB

∴∠AED=∠EBF=∠EFB=∠BFH

又∵∠A=∠FHB=90°，

∴，故②正确；

∵AD=DF=DC，∠DFG=∠C=90°，DG=DG

∴Rt△DFG≌Rt△DCG（HL）

∴FG=CG，

设FG=CG=x，则EG=3+x，BG=6-x，

在Rt△BEG中，由勾股定理得：，

解得：x=2，

∴EG=5，

∴，故③错误；

∵FH⊥BC，

∴△FGH∽△EGB，

∴，即

∴，故④正确；

故答案为：C．