题目内容
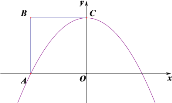
【题目】如图1,抛物线y1=ax2﹣![]() x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,![]() ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
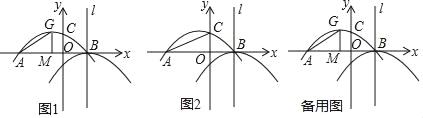
(1)求抛物线y2的解析式;
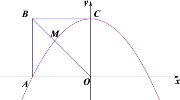
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)应用待定系数法求解析式;
(2)设出点T坐标,表示△TAC三边,进行分类讨论;
(3)设出点P坐标,表示Q、R坐标及PQ、QR,根据以P,Q,R为顶点的三角形与△AMG全等,分类讨论对应边相等的可能性即可.
(1)由已知,c=![]() ,
,
将B(1,0)代入,得:a﹣![]() =0,
=0,
解得a=﹣![]() ,
,
抛物线解析式为y1=![]() x2-
x2-![]() x+
x+![]() ,
,
∵抛物线y1平移后得到y2,且顶点为B(1,0),
∴y2=﹣![]() (x﹣1)2,
(x﹣1)2,
即y2=-![]() x2+
x2+![]() x-
x-![]() ;
;
(2)存在,
如图1:
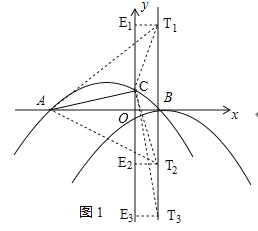
抛物线y2的对称轴l为x=1,设T(1,t),
已知A(﹣3,0),C(0,![]() ),
),
过点T作TE⊥y轴于E,则
TC2=TE2+CE2=12+(![]() )2=t2﹣
)2=t2﹣![]() t+
t+![]() ,
,
TA2=TB2+AB2=(1+3)2+t2=t2+16,
AC2=![]() ,
,
当TC=AC时,t2﹣![]() t+
t+![]() =
=![]() ,
,
解得:t1=![]() ,t2=
,t2=![]() ;
;
当TA=AC时,t2+16=![]() ,无解;
,无解;
当TA=TC时,t2﹣![]() t+
t+![]() =t2+16,
=t2+16,
解得t3=﹣![]() ;
;
当点T坐标分别为(1,![]() ),(1,
),(1,![]() ),(1,﹣
),(1,﹣![]() )时,△TAC为等腰三角形;
)时,△TAC为等腰三角形;
(3)如图2:
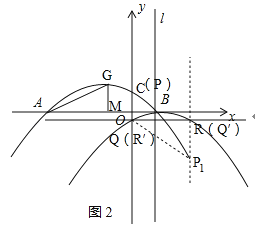
设P(m,![]() ),则Q(m,
),则Q(m,![]() ),
),
∵Q、R关于x=1对称
∴R(2﹣m,![]() ),
),
①当点P在直线l左侧时,
PQ=1﹣m,QR=2﹣2m,
∵△PQR与△AMG全等,
∴当PQ=GM且QR=AM时,m=0,
∴P(0,![]() ),即点P、C重合,
),即点P、C重合,
∴R(2,﹣![]() ),
),
由此求直线PR解析式为y=﹣![]() x+
x+![]() ,
,
当PQ=AM且QR=GM时,无解;
②当点P在直线l右侧时,
同理:PQ=m﹣1,QR=2m﹣2,
则P(2,﹣![]() ),R(0,﹣
),R(0,﹣![]() ),
),
PQ解析式为:y=﹣![]() ;
;
∴PR解析式为:y=﹣![]() x+
x+![]() 或y=﹣
或y=﹣![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】 某校行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生听写结果.以下是根据抽查绘制的统计图的一部分.
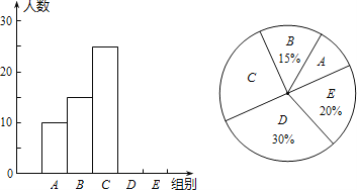
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)这次抽样调查的样本容量是______,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是______;
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.