Question

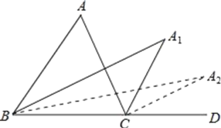
【题目】如图，在△ABC中，∠A=α，∠ABC的平分线与∠ACD的平分线交于点A1，得∠A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，得∠A2，…，∠A2013BC的平分线与∠A2013CD的平分线交于点A2014，得∠A2014CD，则∠A2014=_____．

Answer 1

【答案】.

【解析】

利用角平分线的性质、三角形外角性质，易证∠A1∠A，进而可求∠A1，由于∠A1∠A，∠A2∠A1∠A，…，以此类推可知∠A2014∠A°．

∵A1B平分∠ABC，A1C平分∠ACD，∴∠A1BC∠ABC，∠A1CA∠ACD．

∵∠A1CD=∠A1+∠A1BC，即∠ACD=∠A1∠ABC，∴∠A1（∠ACD﹣∠ABC）．

∵∠A+∠ABC=∠ACD，∴∠A=∠ACD﹣∠ABC，∴∠A1∠A，∠A2∠A1∠A，…，以此类推可知∠A2014∠A°．

故答案为：°．