题目内容
 如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图方式放置,点A1、A2、A3…和点C1、C2、C3…分别在直线y=kx+b(k>0)和x轴上.已知点B1(1,1)、B2(3,2),那么点A4的坐标为
如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图方式放置,点A1、A2、A3…和点C1、C2、C3…分别在直线y=kx+b(k>0)和x轴上.已知点B1(1,1)、B2(3,2),那么点A4的坐标为考点:正方形的性质,一次函数图象上点的坐标特征
专题:规律型
分析:根据点B1、B2的坐标求出点A1、A2的坐标,再利用待定系数法求一次函数解析式求出直线的解析式,再根据一次函数解析式求出点A3的坐标,然后依次求出正方形的边长,并得到后一个正方形的边长是前一个正方形的边长的2倍,求出第四个正方形的边长,再写出A4的坐标,求出第n个正方形的边长,再写出An即可.
解答:解:∵B1(1,1)、B2(3,2),
∴A1(0,1),A2(1,2),
∴
,
解得
,
∴直线解析式为y=x+1,
x=3时,y=4,
∴点A3(3,4),
∴第一个正方形的边长为1,第二个正方形的边长为2,第三个正方形的边长为4,…,
以此类推,后一个正方形的边长是前一个正方形的边长的2倍,
∴第四个正方形的边长是8,
∴A4(7,8),
第n个正方形的边长为2n-1,
∴An(2n-1-1,2n-1).
故答案为:(7,8),(2n-1-1,2n-1).
∴A1(0,1),A2(1,2),
∴
|
解得
|
∴直线解析式为y=x+1,
x=3时,y=4,
∴点A3(3,4),
∴第一个正方形的边长为1,第二个正方形的边长为2,第三个正方形的边长为4,…,
以此类推,后一个正方形的边长是前一个正方形的边长的2倍,
∴第四个正方形的边长是8,
∴A4(7,8),
第n个正方形的边长为2n-1,
∴An(2n-1-1,2n-1).
故答案为:(7,8),(2n-1-1,2n-1).
点评:本题考查了正方形的性质,一次函数图象上点的坐标特征,待定系数法求一次函数解析式,观察并求出后一个正方形的边长是前一个正方形的边长的2倍是解题的关键,要注意点A系列的横坐标比纵坐标小1.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
直角三角形的斜边比一直角边长2cm,另一直角边长为6cm,则它的斜边长( )
| A、4cm | B、8cm |
| C、10cm | D、12cm |
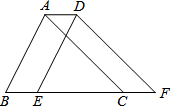 如图,将周长为15cm的△ABC沿射线BC方向平移2cm后得到△DEF,则四边形ABFD的周长为
如图,将周长为15cm的△ABC沿射线BC方向平移2cm后得到△DEF,则四边形ABFD的周长为 一次函数y=2x+4的图象如图,根据图象可知,当x
一次函数y=2x+4的图象如图,根据图象可知,当x