题目内容
20.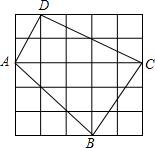 如图,每个小方格的边长都为1.
如图,每个小方格的边长都为1.(1)求图中格点四边形ABCD的面积;
(2)请探究:AD与CD的位置关系,并说明理由.
分析 (1)连接AC,四边形可以把它看成两个三角形,即△ADC,△ABC,再求出其面积的和即可;
(2)可求得AC、CD、AD的长,利用勾股定理的逆定理可判定AD、CD的位置关系.
解答 解:(1)∵S△ADC=5×2÷2=5,S△ABC=5×3÷2=7.5,
∴四边形ABCD的面积=S△ADC+S△ABC=5+7.5=12.5;
(2)由勾股定理,得AD=$\sqrt{5}$,CD=2$\sqrt{5}$,
由题意可知AC=5,
∴AD2+CD2=($\sqrt{5}$)2+(2$\sqrt{5}$)2=25=AC2,
∴△ACD为直角三角形,
∴∠ADC=90°,
∴AD⊥CD.
点评 本题主要考查了三角形的面积以及勾股定理及其逆定理的应用,掌握勾股定理求边长及由三边之间的平方关系判定直角三角形是解题的关键.

练习册系列答案
相关题目
8.为了弘扬传统文化,某校举办了一次国学知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上为合格,达到9分以上(包括9分)为优秀,这次竞赛中,甲、乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
(2)小明对同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是甲(填“甲”或“乙”)组的学生;
(3)甲组同学说他们的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩更好于甲组.请你给出三条支持乙组同学观点的理由.

(1)补充完成下面的成绩统计分析表:
| 组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 甲组 | 6.7 | 6 | 3.4 | 90% | 20% |
| 乙组 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(3)甲组同学说他们的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩更好于甲组.请你给出三条支持乙组同学观点的理由.
15.设一个正方形的边长为acm,若边长增加3cm,则新正方形的面积增加了( )
| A. | 9cm2 | B. | 6acm2 | C. | (6a+9)cm2 | D. | 无法确定 |
10. 小明在所面对的平面镜内看到他背后墙上时钟所成的像如右图所示,则此时的实际时刻应是( )
小明在所面对的平面镜内看到他背后墙上时钟所成的像如右图所示,则此时的实际时刻应是( )
 小明在所面对的平面镜内看到他背后墙上时钟所成的像如右图所示,则此时的实际时刻应是( )
小明在所面对的平面镜内看到他背后墙上时钟所成的像如右图所示,则此时的实际时刻应是( )| A. | 3:30 | B. | 4:30 | C. | 7:30 | D. | 8:30 |

 如图是某农场大棚里三种蔬菜种植面积的扇形统计图,根据所给数据填空
如图是某农场大棚里三种蔬菜种植面积的扇形统计图,根据所给数据填空