题目内容
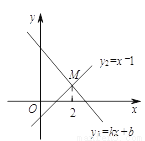
如图,直线y1=kx+b与两坐标轴的正半轴相交,与直线y2=x-1相交于点M,且点M的横坐标为2,则下列结论:①k<0;②kb<0;③当x<2时,y1<y2.其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
C 【解析】由一次函数y1=kx+b的图象经过第一、二、四象限,又由k<0时,直线必经过二、四象限,故知k<0,①正确; 再由图象过一、二象限,即直线与y轴正半轴相交,所以b>0,∴kb<0,②正确; 当x<2时,一次函数y2=x-1在y1=kx+b的图象的下方,故y2<y1,③错误;所以正确的有2个, 故选C.
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目


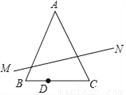
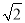 ≈1.41,
≈1.41, 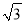 ≈1.73)
≈1.73)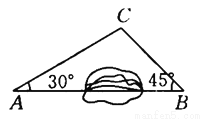
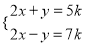 的解满足方程
的解满足方程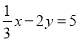 ,则k=_________.
,则k=_________.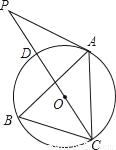
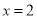 是关于
是关于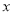 的方程
的方程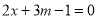 的解,则
的解,则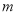 的值等于_____.
的值等于_____.