��Ŀ����
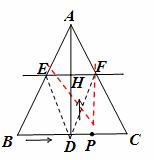
�� ͼ���ڡ�ABC�У�AB=AC��AD��AB��D��BC=10cm��AD=8cm����P�ӵ�B���������߶�BC����ÿ��3cm���ٶ����C�����˶������ͬʱ����ֱ��AD��ֱ��m�ӵױ�BC��������ÿ��2cm���ٶ���DA��������ƽ�ƣ��ֱ�AB��AC��AD��E��F��H������P�����Cʱ����P��ֱ��mͬʱֹͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����t=2ʱ������DE��DF����֤���ı���AEDFΪ���Σ�
��2���������˶������У����γɵġ�PEF������������ֵ������PEF��������ʱ�����߶�BP�ij���
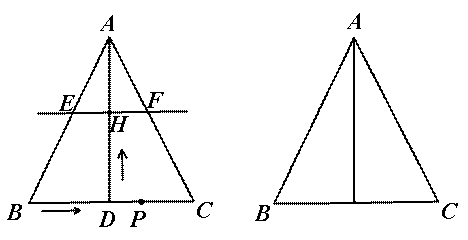 ��3���Ƿ����ijһʱ��t��ʹ��PEFΪֱ�������Σ������ڣ��������ʱ��t��ֵ���������ڣ���˵�����ɡ�
��3���Ƿ����ijһʱ��t��ʹ��PEFΪֱ�������Σ������ڣ��������ʱ��t��ֵ���������ڣ���˵�����ɡ�
��25-1ͼ ��25����ͼ
�⣺��1����t=2ʱ��DH=AH=4����AD��AB��AD��EF��֪EF��BC
�� 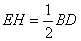 ��
��
�֡� AB=AC��AD��BC
�� BD=CD
�� EH=FH
�� EF��AD���ഹֱƽ��
�� �ı���AEDFΪ����
��2���������DH=2t��AH=8��2t��BC=10cm��AD=8cm����EF��BC֪��AEF�ס�ABC
�� 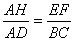 ��
��
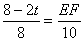 �����
�����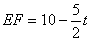
�� 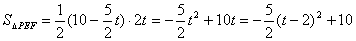
����PEF������������ֵ10cm2����ʱBP=3��2=6cm��
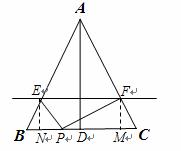
��3����E��F�ֱ���EN��BC��N��EM��BC��M����֪EF =MN=
=MN=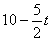
EN=FM����AB=AC��֪BN=CM=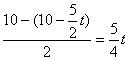
��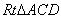 ��
��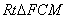 ����
����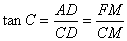 ��
��  ��
��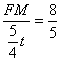 ��
��
���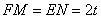 ������
������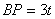 ֪
֪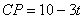 ��
��
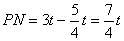 ��
��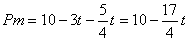
�� 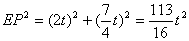 ��
�� 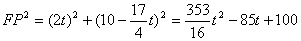
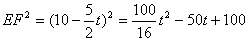
������������ۣ�
������EPF=90�㣬��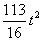
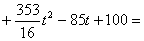
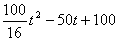 �����
�����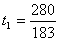 ��
��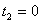 ����ȥ��
����ȥ��
������EFP=90�㣬��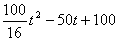
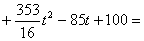
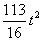 �����
�����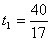 ��
��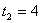 ����ȥ��
����ȥ��
������FEP=90�㣬��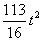

 �����
�����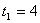 ��
��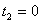 ������ȥ��
������ȥ��
������������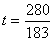
 ��
�� ʱ����PEFΪֱ�������Ρ�
ʱ����PEFΪֱ�������Ρ�

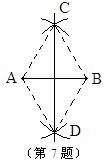

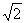 ��1.414��
��1.414��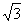 ��1.732��
��1.732��
 �����AEB����
�����AEB����
 ��___________.
��___________. B��
B��
 D��
D��
 �Ľ�Ϊ
�Ľ�Ϊ ��
��