题目内容
18．
（1）画出△ABC关于y轴的对称图形△A1B1C1，并写出△A1B1C1的顶点坐标；（2）在x轴上求作点P，使PA+PC的值最小．
分析 （1）分别作出各点关于y轴的对称点，再顺次连接，根据各点在坐标系中的位置写出各点坐标即可；
（2）作点C关于x轴的对称点C′，连接C′交x轴于点P，则P点即为所求．
解答 
解：（1）如图所示，
由图可知，A1（-3，4），B1（-1，2），C1（-5，1）；
（2）如图，点P即为所求．
点评 本题考查的是作图-轴对称变换，熟知关于y轴对称的点的坐标特点是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．
如图，第一象限的点P的坐标是（a，b），则tan∠POx等于（ ）
如图，第一象限的点P的坐标是（a，b），则tan∠POx等于（ ）| A． | $\frac{a}{b}$ | B． | $\frac{b}{a}$ | C． | $\frac{a}{{\sqrt{{a^2}+{b^2}}}}$ | D． | $\frac{b}{{\sqrt{{a^2}+{b^2}}}}$ |
生物课题研究小组对附着在物体表面的三个微生物（课题组成员把他们分别标号为1，2，3）的生长情况进行观察记录，这三个微生物第一天各自一分为二，产生新的微生物（依次被标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录），那么标号为1535的微生物会出现在（ ）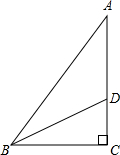
如图，在Rt△ABC中，∠C=90°，BD是三角形的角平分线，交AC于点D，AD=2.2cm，AC=3.7cm，则点D到AB边的距离是1.5cm．
如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，AC=13，BC=5，BE⊥DC交DC的延长线于点E．
如图是由几个相同的小正方体搭成的立体图形，则从它的上面看到的图形是
．