��Ŀ����
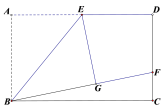
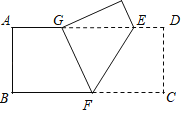
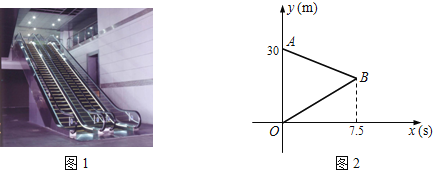
����Ŀ����ͼ1��ij�̳���һ˫�����е��Զ����ݣ��������к����е��ٶȱ��ֲ�������ͬ���ס�������ͬʱվ���˴˷��ݵ����к����жˣ���վ�����з��ݵ�ͬʱ����0.8 m/s���ٶ������ܣ���վ�����з��ݺ���վ��������������У�������;��������������ݶ��˺������������з��ݣ�ͬʱ��0.8 m/s���ٶ������ܣ����ҵ���˺�����ԭ�صȺ�ף�ͼ2���߶�OB��AB�ֱ��ʾ�ס��������ڳ������ݹ����У�����ݵ˵�·��y��m��������ʱ��x��s��֮��IJ��ֺ�����ϵ�����ͼ�����������⣺
��1����B�������� ��
��2����AB����ֱ�ߵĺ�����ϵʽ��
��3���ҵ�����ݵ˺���ȴ��ʱ�䣬�ײŵ�����ݵˣ�
���𰸡���1����7.5��18��;��2��AB����ֱ�ߵĺ�����ϵʽΪy����1.6x��30;��3����ȴ���ʱ��Ϊ6.25s
��������
��1������������к����е��ٶ�Ϊxm/s����������ʱ·�̺�Ϊ30�����з���7.5��2x+0.8��=30����÷������к����е��ٶȣ��Ӷ���⣻
��2�����һ�κ�����һ����ʽ����A��B�������꣬�������ֱ��AB�ĺ�����ϵʽ��
��3���ֱ���üס�������������ʱ�䣬���������⣮
��1����������к����е��ٶ�Ϊxm/s����
7.5��2x+0.8��=30��
���x=1.6��
7.5��x+0.8��=7.5����1.6+0.8��=7.5��2.4=18��
���B�������� ��7.5��18����
��B��7.5��18����
��2����ֱ��AB�ĺ�����ϵʽΪy=kx+b��
��A��B����ֱ�Ϊ��0��30������7.5��18�����룺y=kx+b���ã�
![]() ��
��
��ã� ��
��
��AB����ֱ�ߵĺ�����ϵʽΪy=-1.6x+30��
��3�������⣬��
30��2����1.6+0.8��-30��1.6
=60��2.4-18.75
=25-18.75
=6.25��s����
���ҵ�����ݵ˺���ȴ�6.25s���ײŵ�����ݵˣ�

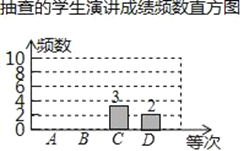
����Ŀ��ijУΪ��ף�����������������2018��4�µ���֯��Уѧ���ٰ������������ľ�����г�����������ݽ�������Ϊ�˽�ѧ�����ݽ������еijɼ������ѧУ�����ȡ�˲���ѧ�����ݽ������ɼ�����ͳ��(���֣�100�֣��ȴΣ�A�����㣺90��100�֣�B�����ã�80��89�֣�C��һ�㣺60��79�֣�D���ϲ60�����£�����60��)�õ����²�������ͼ����
�ȴ� | Ƶ�� | Ƶ�� |
A | a | 0.25 |
B | b | 0.5 |
C | 3 | m |
D | 2 | 0.1 |
����������Ϣ�����������
(1)����a��_____��b��_____��m��_______������ȫƵ���ֲ�ֱ��ͼ��
(2)���ݳ��ѧ���ݽ��ɼ�Ƶ��ͳ�Ʊ�����������ͳ��ͼ�У���ʾC�ȴβ��ֵ��������ĽǵĶ�����_______��
(3)��A�ȴ�����2��Ů��������Ϊ������ѧУ����A�ȴ�ѧ���г�ȡ2��ѧ������ݽ���ϲμ�ȫ�����������걭���ݽ���������ǡ�ó�ȡ1��������1��Ů���ĸ��ʣ�