题目内容
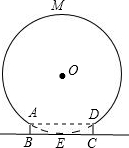
我们在园林游玩时,常见到如图所示的圆弧形的门,若圆弧所在圆与地面BC相切于E点,四边形ABCD是一个矩形.已知AB= 米,BC=1米.
米,BC=1米.(1)求圆弧形门最高点到地面的距离;
(2)求弧AMD的长.

【答案】分析:(1)根据题意,所求距离就是圆的直径,所以可以连接半径作弦心距来构造直角三角形.
(2)求弧长,关键在于求圆心角,根据直角三角形求出圆心角后代入弧长公式就解决了.
解答: 解:(1)设圆弧所在圆的圆心为O,
解:(1)设圆弧所在圆的圆心为O,
连接OE交AD于F,连接OA,如图所示:
设⊙O半径为x,
则OF=x- 米,AF=
米,AF= 米
米
在Rt△AOF中x2=( )2+(x-
)2+(x- )2
)2
解得:x=1
圆弧门最高点到地面的距离为2米.
(2)∵OA=1,OF=1- =
=
∴∠AOF=30°∴∠AOD=60°(8分)
弧AMD的长= =
= 米.
米.
点评:构造直角三角形,利用勾股定理是求解本题的关键.
(2)求弧长,关键在于求圆心角,根据直角三角形求出圆心角后代入弧长公式就解决了.
解答:
 解:(1)设圆弧所在圆的圆心为O,
解:(1)设圆弧所在圆的圆心为O,连接OE交AD于F,连接OA,如图所示:
设⊙O半径为x,
则OF=x-
 米,AF=
米,AF= 米
米在Rt△AOF中x2=(
 )2+(x-
)2+(x- )2
)2解得:x=1
圆弧门最高点到地面的距离为2米.
(2)∵OA=1,OF=1-
 =
=
∴∠AOF=30°∴∠AOD=60°(8分)
弧AMD的长=
 =
= 米.
米.点评:构造直角三角形,利用勾股定理是求解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 我们在园林游玩时,常见到如图所示的圆弧形的门,若圆弧所在圆与地面BC相切于E点,四边形ABCD是一个矩形.已知AB=
我们在园林游玩时,常见到如图所示的圆弧形的门,若圆弧所在圆与地面BC相切于E点,四边形ABCD是一个矩形.已知AB= 我们在园林游玩时,常见到如图所示的圆弧形的门,若圆弧所在圆与地面BC相切于E点,四边形ABCD是一个矩形.已知AB=
我们在园林游玩时,常见到如图所示的圆弧形的门,若圆弧所在圆与地面BC相切于E点,四边形ABCD是一个矩形.已知AB=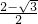 米,BC=1米.
米,BC=1米.
 米,BC=1米.
米,BC=1米.
 米,BC=1米.
米,BC=1米.