题目内容
10.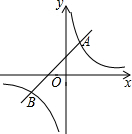 如图,已知一次函数y1=k1x+b(k1为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象相交于A(1,2),B(m,-1)两点.
如图,已知一次函数y1=k1x+b(k1为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象相交于A(1,2),B(m,-1)两点.(1)求一次函数和反比例函数的解析式;
(2)若A1(m1,n1),A(m2,n2),A3(m3,n3)为反比例函数图象上的三点,且m1<m2<0<m3,请直接写出n1、n2、n3的大小关系式;
(3)结合图象,请直接写出关于x的不等式k1x+b>$\frac{{k}_{2}}{x}$的解集.
分析 (1)根据待定系数法即可解决.
(2)画出图象即可.
(3)不等式k1x+b>$\frac{{k}_{2}}{x}$的解集在图象上是直线在上面的部分,根据图象即可写出.
解答 (1)解:∵反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象经过A(1,2),B(m,-1)
∴k2=2,m=-2,
∵一次函数y1=k1x+b(k1为常数,且k1≠0)的图象经过A(1,2),B(-2,-1),
∴$\left\{\begin{array}{l}{{k}_{1}+b=2}\\{-2{k}_{1}+b=-1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{k}_{1}=1}\\{b=1}\end{array}\right.$,
∴一次函数和反比例函数的解析式分别为y=x+1,y=$\frac{2}{x}$.
(2)由图象可知:n3>n1>n2.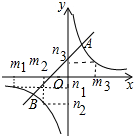
(3)由图象可知,不等式k1x+b>$\frac{{k}_{2}}{x}$的解集为:-2<x<0或x>1.
点评 本题考查一次函数与反比例函数的有关知识,学会用待定系数法求函数解析式,掌握由图象根据要求确定自变量的取值范围的方法,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
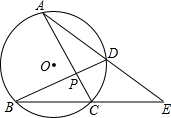 如图,AC与BD交于P,AD、BC延长交于点E,∠AEC=37°,∠CAE=31°,则∠APB的度数为99°.
如图,AC与BD交于P,AD、BC延长交于点E,∠AEC=37°,∠CAE=31°,则∠APB的度数为99°.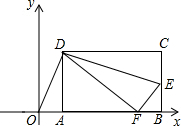 如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(6,8),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点E的坐标为(16,3)或(4$\sqrt{5}$+6,2$\sqrt{5}$-2)或($\frac{43}{3}$,$\frac{7}{4}$).
如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(6,8),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点E的坐标为(16,3)或(4$\sqrt{5}$+6,2$\sqrt{5}$-2)或($\frac{43}{3}$,$\frac{7}{4}$).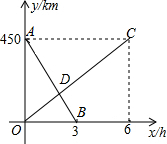 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示;慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段0C所示.根据图象进行以下研究.
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示;慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段0C所示.根据图象进行以下研究.