题目内容
19.边长为13的菱形,一条对角线长为10,则菱形的面积为120.分析 根据菱形的对角线互相垂直平分,得已知对角线的一半是5.根据勾股定理,得要求的对角线的一半是12,则另一条对角线的长是24,进而求出菱形的面积.
解答 解:在菱形ABCD中,AB=13,AC=10,
∵对角线互相垂直平分,
∴∠AOB=90°,AO=5,
在RT△AOB中,BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=12,
∴BD=2BO=24.
∴则此菱形面积是$\frac{1}{2}$×10×24=120,
故答案为:120.
点评 本题考查了菱形的性质,熟记菱形对角线的性质:菱形的对角线互相垂直平分和熟练运用勾股定理是解题关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
14.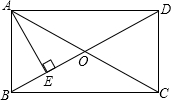 如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )
 如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为( )| A. | 6 | B. | 5 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
8.下面四个图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
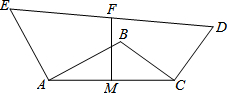 如图,AE⊥AB,BC⊥CD,且AE=AB,BC=CD,F为DE的中点,M为AC中点,证明:FM⊥AC.
如图,AE⊥AB,BC⊥CD,且AE=AB,BC=CD,F为DE的中点,M为AC中点,证明:FM⊥AC.