题目内容
11．已知关于x的方程x2+（m-1）x+4=0有两个相等的实数根，求m的值．分析 由方程有两个相等的实数根，得到根的判别式等于0，列出关于m的方程，求出方程的解即可得到m的值．
解答 解：∵方程x2+（m-1）x+4=0有两个相等的实数根，
∴△=b2-4ac=（m-1）2-4×1×4=0，
解得：m1=5，m2=-3．
故m的值为5或-3．
点评 此题考查了一元二次方程根的判别式，当根的判别式的值大于0，一元二次方程有两个不相等的实数根；当根的判别式等于0，一元二次方程有两个相等的实数根；当根的判别式小于0，一元二次方程没有实数根．
练习册系列答案
相关题目
19．分式$\frac{35{a}^{2}{b}^{2}}{15{a}^{3}bc}$约分的结果是（ ）
| A． | $\frac{7b}{3a}$ | B． | $\frac{7b}{3ac}$ | C． | $\frac{3a}{7b}$ | D． | $\frac{3ac}{7b}$ |
6．方程3x2-x+1=0的二次项系数和一次项系数分别为（ ）
| A． | 3和0 | B． | 3和-1 | C． | 2和-1 | D． | 3和1 |
16．下列说法正确的是（ ）
| A． | 正有理数和负有理数统称为有理数 | |
| B． | 符号不同的两个数互为相反数 | |
| C． | 绝对值等于它的相反数的数是非正数 | |
| D． | 两数相加，和一定大于任何一个加数 |
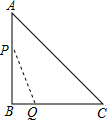如图，在△ABC中，∠B=90°，AB=BC=4，动点P从点A出发沿A→B→C运动，动点Q从点B出发沿B→C→A运动．如果P、Q两点同时出发，速度均为1个单位/秒．设出发时间为x秒（0≤x≤8），记△PBQ的面积y1的函数图象为T．若直线y2=x+b与T只有一个交点，则b的取值范围为b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8＜b＜0或b=$\frac{1}{2}$．