题目内容
16. 如图,点O是△ABC的∠ABC、∠ACB平分线的交点
如图,点O是△ABC的∠ABC、∠ACB平分线的交点(1)如果∠A=60°,则∠BOC=120°;
(2)当∠A有大小发生变化时,∠BOC会不会等于90°?为什么?
分析 (1)根据∠A的度数,可得出∠ABC+∠ACB的度数,再由OB,OC是角平分线,可得出∠BOC的度数;
(2)当∠BOC等于90°时,$\frac{1}{2}$(∠ABC+∠ACB)的度数为90度,∠ABC+∠ACB的度数为180°,这是不可能的.
解答 解:(1)∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∴$\frac{1}{2}$(∠ABC+∠ACB)=60°,
即∠BCO+∠CBO=60°,
∴∠BOC=180°-60°=120°,
故答案为:120;
(2)∠BOC不能等于90°,
∵∠BOC=90°+$\frac{1}{2}$∠A,(0<n<180°),
∴∠BOC不能等于90°.
点评 本题考查了三角形的内角和定理,本题是一个由简单到复杂,由特殊到一般的题目,难度不大,掌握做题的方法和思路即可.

练习册系列答案
相关题目
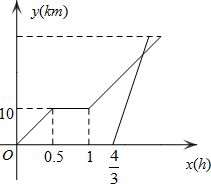 周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后达到甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同的路线前往乙地,他们离家的路程y(km)与小明离家时间x(h)之间的关系如图所示,已知妈妈驾车的速度是小明汽车速度的3倍
周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后达到甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同的路线前往乙地,他们离家的路程y(km)与小明离家时间x(h)之间的关系如图所示,已知妈妈驾车的速度是小明汽车速度的3倍