题目内容
如果两个等腰三角形的顶角相等,周长相等,求证:这两个三角形全等.
考点:全等三角形的判定,等腰三角形的性质
专题:证明题
分析:延长BC到N,使AC=CN,延长CB到M,使BM=AB,连接AN、AM,延长EF到W,使DF=FW,延长FE到Q,使EQ=DE,连接DQ、DW,求出MN=QW,∠M=∠Q=∠N=∠W,∠MAB=∠QDE,根据ASA推出△AMN≌△DQW,求出DQ=AM,再根据ASA推出△ABM≌△DEQ,求出AB=DE,AC=DF,根据全等三角形的判定推出即可.
解答: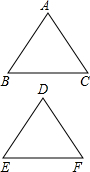 已知:△ABC和△DEF是等腰三角形,AB=AC,DE=DF,∠A=∠D,AB+AC+BC=DE+DF+EF,
已知:△ABC和△DEF是等腰三角形,AB=AC,DE=DF,∠A=∠D,AB+AC+BC=DE+DF+EF,
求证:△ABC≌△DEF,
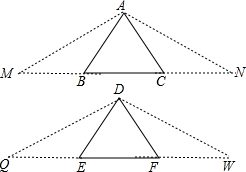
证明:如图,延长BC到N,使AC=CN,延长CB到M,使BM=AB,连接AN、AM,延长EF到W,使DF=FW,延长FE到Q,使EQ=DE,连接DQ、DW,
∵AB+AC+BC=DE+DF+EF,
∴MN=QW,
∵AB=AC,DE=DF,∠A=∠D,
∴∠ABC=∠ACB=∠DEF=∠DFW
 ∵AB=BM,
∵AB=BM,
∴∠M=∠MAB,
∵∠M+∠MAB=∠ABC,
∴∠M=∠MAB=
∠ABC,
同理:∠N=∠NAC=
∠ACB,∠Q=∠QDE=
∠DEF,∠W=∠WDF=
∠DFE,
∴∠M=∠Q=∠N=∠W,∠MAB=∠QDE,
在△AMN和△DQW中,
,
∴△AMN≌△DQW(ASA),
∴DQ=AM,
在△ABM和△DEQ中,
,
∴△ABM≌△DEQ(ASA),
∴AB=DE,
∵AB=AC,DE=DF,
∴AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
 已知:△ABC和△DEF是等腰三角形,AB=AC,DE=DF,∠A=∠D,AB+AC+BC=DE+DF+EF,
已知:△ABC和△DEF是等腰三角形,AB=AC,DE=DF,∠A=∠D,AB+AC+BC=DE+DF+EF,求证:△ABC≌△DEF,
证明:如图,延长BC到N,使AC=CN,延长CB到M,使BM=AB,连接AN、AM,延长EF到W,使DF=FW,延长FE到Q,使EQ=DE,连接DQ、DW,
∵AB+AC+BC=DE+DF+EF,
∴MN=QW,
∵AB=AC,DE=DF,∠A=∠D,
∴∠ABC=∠ACB=∠DEF=∠DFW
 ∵AB=BM,
∵AB=BM,∴∠M=∠MAB,
∵∠M+∠MAB=∠ABC,
∴∠M=∠MAB=
| 1 |
| 2 |
同理:∠N=∠NAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠M=∠Q=∠N=∠W,∠MAB=∠QDE,
在△AMN和△DQW中,
|
∴△AMN≌△DQW(ASA),
∴DQ=AM,
在△ABM和△DEQ中,
|
∴△ABM≌△DEQ(ASA),
∴AB=DE,
∵AB=AC,DE=DF,
∴AC=DF,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SAS).
点评:本题考查了全等三角形的性质和判定的应用,解此题的关键是能正确作出辅助线,题目比较好,有一定的难度.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
△ABC中,∠C=90°,AB=4,cosA=
,则BC的长( )
8
| ||
| 3 |
| A、3 | ||
| B、4 | ||
| C、5 | ||
D、
|
大于-3而小于3的整数有( )个.
| A、5 | B、6 | C、7 | D、8 |
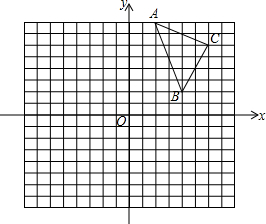 如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).
如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).