题目内容
等腰三角形的腰长为5cm,一腰上的中线将其周长分成两部分的差为1cm,则底边的高为_____cm.
- A.5cm或4cm
- B.4cm或6cm
- C.4cm或
 cm
cm - D.
 cm或2.5cm
cm或2.5cm
C
分析:等腰三角形一腰上的中线将它的周长分成两部分的差为1,但已知没有明确等腰三角形被中线分成的两部分,那一部分大,那一部分小,因此,有两种情况,需要分类讨论.
解答: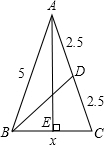 解:根据题意画出图形,如图
解:根据题意画出图形,如图
等腰三角形的腰长AB=AC=5,BC=x,
∵BD是腰上的中线,
∴AD=DC=2.5,
若(AB+AD)-(BC+CD)=1,则7.5-2.5-x=1,解得x=4,
根据勾股定理可求得底边上的高AE= ;
;
若(BC+CD)-(AB+AD)=1,则x-5=1,解得x=6,
根据勾股定理可求得底边上的高AE=3;
所以底边上的高可能为 ,也可能为3.
,也可能为3.
点评:本题考查了等腰三角形的性质;在解决与等腰三角形有关的问题,由于等腰所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错.
分析:等腰三角形一腰上的中线将它的周长分成两部分的差为1,但已知没有明确等腰三角形被中线分成的两部分,那一部分大,那一部分小,因此,有两种情况,需要分类讨论.
解答:
 解:根据题意画出图形,如图
解:根据题意画出图形,如图等腰三角形的腰长AB=AC=5,BC=x,
∵BD是腰上的中线,
∴AD=DC=2.5,
若(AB+AD)-(BC+CD)=1,则7.5-2.5-x=1,解得x=4,
根据勾股定理可求得底边上的高AE=
 ;
;若(BC+CD)-(AB+AD)=1,则x-5=1,解得x=6,
根据勾股定理可求得底边上的高AE=3;
所以底边上的高可能为
 ,也可能为3.
,也可能为3.点评:本题考查了等腰三角形的性质;在解决与等腰三角形有关的问题,由于等腰所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目