题目内容
2.代数式1-$\sqrt{3m-1}$有意义,则m的取值范围是m≥$\frac{1}{3}$.分析 根据二次根式有意义的条件,可得3m-1≥0,然后根据一元一次不等式的解法,求出m的取值范围即可.
解答 解:∵代数式1-$\sqrt{3m-1}$有意义,
∴3m-1≥0,
解得m≥$\frac{1}{3}$,
∴m的取值范围是m≥$\frac{1}{3}$.
故答案为:m≥$\frac{1}{3}$.
点评 此题主要考查了二次根式有意义的条件,要熟练掌握,解答此题的关键是要明确:二次根式中的被开方数是非负数.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
17.下列根式中,是最简二次根式的为( )
| A. | $\sqrt{8a}$ | B. | $\sqrt{{a}^{2}+{b}^{2}}$ | C. | $\sqrt{0.1x}$ | D. | $\sqrt{{a}^{5}}$ |
7.如果把$\frac{x}{x-y}$中的x与y都扩大为原来的10倍,那么这个代数式的值( )
| A. | 不变 | B. | 扩大为原来的5倍 | ||
| C. | 扩大为原来的10倍 | D. | 缩小为原来的$\frac{1}{10}$ |
12.下列说法中,正确的是( )
| A. | 若两条直线被第三条直线所截,则同旁内角互补 | |
| B. | 相等的角是对顶角 | |
| C. | 三角形的外角等于两个内角的和 | |
| D. | 若三条直线两两相交,则共有6对对顶角 |
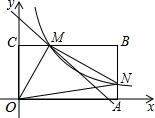 如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线y=-x+6交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线y=$\frac{k}{x}$(x>0)交边AB于点N.若△OAN的面积是4,求△OMN的面积.
如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线y=-x+6交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线y=$\frac{k}{x}$(x>0)交边AB于点N.若△OAN的面积是4,求△OMN的面积.