题目内容
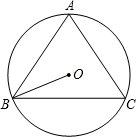 已知:如图,BC是⊙O的弦,点A在⊙O上,AB=AC=10,sin∠ABC=
已知:如图,BC是⊙O的弦,点A在⊙O上,AB=AC=10,sin∠ABC=| 4 | 5 |
求:(1)弦BC的长;(2)∠OBC的正切的值.
分析:(1)根据圆心角定理,得出
=
,利用三角函数关系求出AD的长,进而求出BC的长;
(2)设⊙O的半径OB=r,由OA=OB=r,得OD=8-r,利用勾股定理得出r的长,从而求出∠OBC的正切的值.
 |
| AB |
 |
| AC |
(2)设⊙O的半径OB=r,由OA=OB=r,得OD=8-r,利用勾股定理得出r的长,从而求出∠OBC的正切的值.
解答: 解:(1)连接AO,AO的延长线与弦BC相交于点D.
解:(1)连接AO,AO的延长线与弦BC相交于点D.
在⊙O中,∵AB=AC,
∴
=
.
又∵AD经过圆心O,
∴AD⊥BC,BC=2BD.
在Rt△ABD中,AB=10,sin∠ABC=
,
∴AD=ABsin∠ABC=10×
=8.
于是,由勾股定理得:
BD=
=
=6.
∴BC=12.
(2)设⊙O的半径OB=r.
在⊙O中,由OA=OB=r,得OD=8-r.
在Rt△OBD中,利用勾股定理,得BD2+OD2=OB2,
即得36+(8-r)2=r2.
解得r=
.
∴OB=
.
∴OD=8-
=
.
∴tan∠OBC=
=
=
.
 解:(1)连接AO,AO的延长线与弦BC相交于点D.
解:(1)连接AO,AO的延长线与弦BC相交于点D.在⊙O中,∵AB=AC,
∴
 |
| AB |
 |
| AC |
又∵AD经过圆心O,
∴AD⊥BC,BC=2BD.
在Rt△ABD中,AB=10,sin∠ABC=
| 4 |
| 5 |
∴AD=ABsin∠ABC=10×
| 4 |
| 5 |
于是,由勾股定理得:
BD=
| AB2-AD2 |
| 102-82 |
∴BC=12.
(2)设⊙O的半径OB=r.
在⊙O中,由OA=OB=r,得OD=8-r.
在Rt△OBD中,利用勾股定理,得BD2+OD2=OB2,
即得36+(8-r)2=r2.
解得r=
| 25 |
| 4 |
∴OB=
| 25 |
| 4 |
∴OD=8-
| 25 |
| 4 |
| 7 |
| 4 |
∴tan∠OBC=
| OD |
| BD |
| ||
| 6 |
| 7 |
| 24 |
点评:此题主要考查了勾股定理的应用以及三角函数的应用,综合性较强,也是中考中热点问题,做题过程中应特别注意.

练习册系列答案
相关题目
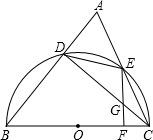 已知:如图,BC是半圆O的直径,D、E是半圆O上两点,
已知:如图,BC是半圆O的直径,D、E是半圆O上两点, 19、已知:如图,BC是等腰△BED底边ED上的高,四边形ABEC是平行四边形.
19、已知:如图,BC是等腰△BED底边ED上的高,四边形ABEC是平行四边形. 已知,如图,BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,若AD:DB=2:3,AC=10.求sinB的值.
已知,如图,BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,若AD:DB=2:3,AC=10.求sinB的值.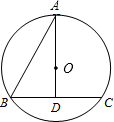 ,
, 已知:如图,BC是△ABC和△DCB的公共边,AC=BD,∠DBC=∠ACB,AE、DF分别垂直BC于E,F.求证:AE=DF.
已知:如图,BC是△ABC和△DCB的公共边,AC=BD,∠DBC=∠ACB,AE、DF分别垂直BC于E,F.求证:AE=DF.