题目内容
16.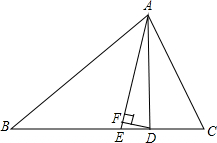 △ABC中,∠B=30°,∠C=58°,AE平分∠BAC,AD⊥BC于D,DF⊥AE于F,求∠ADF.
△ABC中,∠B=30°,∠C=58°,AE平分∠BAC,AD⊥BC于D,DF⊥AE于F,求∠ADF.
分析 根据三角形内角和定理求出∠BAC,根据角平分线定义求出∠CAE,根据三角形内角和定理求出∠CAD,求出∠DAE,根据三角形内角和定理求出即可.
解答 解:∵在△ABC中,∠B=30°,∠C=58°,
∴∠BAC=180°-∠B-∠C=92°,
∵AE平分∠BAC,
∴∠CAE=$\frac{1}{2}∠$BAC=$\frac{1}{2}×$92°=46°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=90°-∠C=90°-58°°=32°,
∴∠DAF=∠CAE-∠CAD=46°-32°=14°,
∵DF⊥AE,
∴∠AFD=90°,
∴∠ADF=90°-∠DAE=90°-14°=76°.
点评 本题考查了三角形内角和定理,垂直定义,角平分线性质的应用,能根据三角形的内角和定理求出各个角的度数是解此题的关键,注意:三角形的内角和等于钱180°.

练习册系列答案
相关题目
4.下列方程:①$2x-\frac{y}{3}=1$;②$\frac{x}{2}+\frac{3}{y}=3$;③x2-y2=4;④5(x+y)=7(x+y);⑤2x+5=6.其中二元一次方程有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、4的四块),你认为将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带( )
小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、4的四块),你认为将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带( )