题目内容
已知关于x的一元二次方程x2-kx-1=0有两个实数根x1,x2,是否存在实数k,使得x1x2-x1-x2=0成立?若存在,请求出k的值;若不存在,请说明理由.
考点:根与系数的关系,根的判别式
专题:存在型
分析:根据根与系数的关系得到x1+x2=k,x1x2=-1,再利用x1x2-x1-x2=0可得-1-k=0,解得k=-1,然后根据判别式的意义判断k的值是否满足条件.
解答:解:存在.
根据题意得x1+x2=k,x1x2=-1,
∵x1x2-x1-x2=0,即x1x2-(x1+x2)=0,
∴-1-k=0,
∴k=-1,
∵k=-1时,△=(-k)2-4×(-1)>0,
∴存在实数k=-1,使得x1x2-x1-x2=0.
根据题意得x1+x2=k,x1x2=-1,
∵x1x2-x1-x2=0,即x1x2-(x1+x2)=0,
∴-1-k=0,
∴k=-1,
∵k=-1时,△=(-k)2-4×(-1)>0,
∴存在实数k=-1,使得x1x2-x1-x2=0.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一艘轮船以18海里/小时的速度由南向北航行,在A处测得小岛P在北偏西15°的方向上,两小时后,轮船在B处测得小岛P在北偏西30°的方向上,已知小岛周围20海里内有暗礁,若轮船仍按原来方向继续前行,有无触礁的危险?
一艘轮船以18海里/小时的速度由南向北航行,在A处测得小岛P在北偏西15°的方向上,两小时后,轮船在B处测得小岛P在北偏西30°的方向上,已知小岛周围20海里内有暗礁,若轮船仍按原来方向继续前行,有无触礁的危险?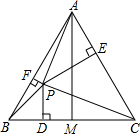 如图,P是等边△ABC内任意一点,由P向边BC、AC、AB分别引垂线段PD、PE、PF,AM⊥BC,AM=6cm,则PD+PE+PF=
如图,P是等边△ABC内任意一点,由P向边BC、AC、AB分别引垂线段PD、PE、PF,AM⊥BC,AM=6cm,则PD+PE+PF=