题目内容
一圆周上有三点A，B，C，∠A的平分线交边BC于D，交圆于E，已知BC=2，AC=3，AB=4，则AD•DE= ．
【答案】分析：根据角平分线的性质得出
，求出BD与CD的长，再利用相交弦定理求出即可．
解答：解：∵∠A的平分线交边BC于D，交圆于E，
∴
，
∵BC=2，AC=3，AB=4，
∴
，
解得：BD=
，CD=2-
=
，
∵CD•BD=AD•DE=
×
=
．
故答案为：
．
点评：此题主要考查了相交弦定理以及角平分线的性质，根据角平分线性质得出
，是解决问题的关键．
，求出BD与CD的长，再利用相交弦定理求出即可．解答：解：∵∠A的平分线交边BC于D，交圆于E，
∴
，∵BC=2，AC=3，AB=4，
∴
，解得：BD=
，CD=2-=，∵CD•BD=AD•DE=
×=．故答案为：
．点评：此题主要考查了相交弦定理以及角平分线的性质，根据角平分线性质得出
，是解决问题的关键． 
练习册系列答案
相关题目
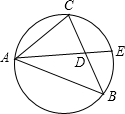一圆周上有三点A，B，C，∠A的平分线交边BC于D，交圆于E，已知BC=2，AC=3，AB=4，则AD•DE=
（2011•潍城区模拟）如图是一个圆形的街心花园，A、B、C是圆周上的三个娱乐点，且A、B、C三等分圆周，街心花园内除了沿圆周的一条主要道路外还有经过圆心的
一圆周上有三点A，B，C，∠A的平分线交边BC于D，交圆于E，已知BC=2，AC=3，AB=4，则AD•DE=________．