Question

10．如图，已知AB为⊙O直径，AC是⊙O的弦，∠BAC的平分线AD交⊙O于D，过点D作DE⊥AC交AC的延长线于点E，OE交AD于点F，cos∠BAC=$\frac{3}{5}$
（1）求证：DE是⊙O的切线；
（2）若AF=8，求DF的长．

Answer 1

分析 （1）连接OD，推出OD∥AE，推出OD⊥DE，根据切线判定推出即可；
（2）连接BD，过D作DH⊥AB于H，根据cos∠DOH=cos∠CAB=$\frac{AC}{AB}$=$\frac{3}{5}$，设OD=5x，则 AB=10x，OH=3x，DH=4x．由勾股定理得：AD²=80x²，证△EAD∽△DAB求出AD²=AE•AB=AE•10x，得出AE=8x，根据△ODF∽△EAF即可得到结论．

解答 （1）证明：连接OD，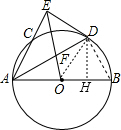
∵OA=OD，
∴∠ODA=∠OAD，
∵AD平分∠BAC，
∴∠CAD=∠OAD，
∴∠CAD=∠ODA，
∴OD∥AC，
∵AE⊥DE，
∴OD⊥DE，
∵OD为半径，
∴DE是⊙O切线；

（2）解：过D作DH⊥AB于H，连接BD、OD，
则∠CAB=∠DOH，
∵cos∠DOH=cos∠CAB=$\frac{AC}{AB}$=$\frac{3}{5}$，
设OD=5x，则 AB=10x，OH=3x，DH=4x．
在Rt△ADH中，由勾股定理得：AD²=（4x）²+（5x+3x）²=80x²，
∵DE⊥AC，AB是⊙O直径，
∴∠AED=∠ADB=90°，
∵∠EAD=∠BAD（角平分线定义），
∴△EAD∽△DAB，
∴$\frac{AE}{AD}=\frac{AD}{AB}$，
∴AD²=AE•AB=AE•10x，
∴AE=8x，
∵OD∥AE，
∴△ODF∽△EAF，
∴$\frac{AF}{DF}=\frac{AE}{OD}$=$\frac{8x}{5x}$=$\frac{8}{5}$，
∵AF=8，
∴DF=5．

点评 本题考查了平行线判定和性质，切线判定，相似三角形的性质和判定，解直角三角形，勾股定理等知识点的应用，主要考查学生的推理和计算能力．