题目内容
12．解不等式组$\left\{\begin{array}{l}{2x+1＞0}\\{x＞2x-5}\end{array}\right.$．分析 首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．
解答 解：$\left\{\begin{array}{l}{2x+1＞0…（1）}\\{x＞2x-5…（2）}\end{array}\right.$，
由（1）得：x＞-$\frac{1}{2}$
由（2）得：x＜5
综合得不等式组的解集为-$\frac{1}{2}$＜x＜5．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
阅读快车系列答案
相关题目
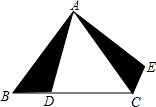如图，△ABC是等边三角形，D是BC边上的一点，△ACE是由△ABD绕A逆时针旋转一定角度得到的对应三角形，那么BD旋转到CE的旋转角度数为60°．
3．3.14159、-$\root{3}{343}$、0.13113113、-π这四个实数中无理数的个数是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 | ||||
| E． | 4 |
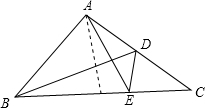已知在△ABC中，∠BAC=90°，AB=AC，D是AC的中点，AE⊥BD交BC于E，求证：BD=AE+DE．（提示：过点A作BC的垂线交BD于H）
1．下列各式计算不正确的是（ ）
| A． | 22•23=25 | B． | ${（-2）^{-1}}=-\frac{1}{2}$ | C． | （25）5=225 | D． | $\sqrt{（1-\sqrt{2}{）^2}}=1-\sqrt{2}$ |