题目内容
在RT△ABC中,∠C=90°,BC=a,AC=b,求△ABC的内切圆⊙O的半径.
考点:三角形的内切圆与内心
专题:计算题
分析:先利用勾股定理计算出AB,然后根据直角边为a、b,斜边为c的三角形的内切圆半径为
求解.
| a+b-c |
| 2 |
解答:解:∵∠C=90°,BC=a,AC=b,
∴AB=
,
∴△ABC的内切圆⊙O的半径=
.
∴AB=
| a2+b2 |
∴△ABC的内切圆⊙O的半径=
a+b-
| ||
| 2 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.记住直角边为a、b,斜边为c的三角形的内切圆半径为
.
| a+b-c |
| 2 |

练习册系列答案
相关题目
 如图,求∠1+∠2的值.
如图,求∠1+∠2的值. 如图,一个无盖的长方体长、宽、高分别为8cm、8cm、12cm,一只蚂蚁从A爬到C1,怎样爬路线最短,最短路径是多少?
如图,一个无盖的长方体长、宽、高分别为8cm、8cm、12cm,一只蚂蚁从A爬到C1,怎样爬路线最短,最短路径是多少?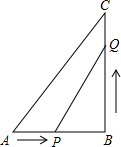 如图,△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
如图,△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.