题目内容
 如图,以点M(1,2)为圆心的圆交y轴于A、B两点,点A的坐标为(0,1),则点B的坐标为________.
如图,以点M(1,2)为圆心的圆交y轴于A、B两点,点A的坐标为(0,1),则点B的坐标为________.
(0,3)
分析:连接MB、MA,过点M作MN⊥AB于点N.根据垂径定理、勾股定理求得BN=AN= AB=1;然后由坐标与图形的性质求得点B的纵坐标.
AB=1;然后由坐标与图形的性质求得点B的纵坐标.
解答: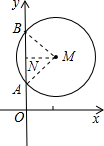 解:连接MB、MA,过点M作MN⊥AB于点N;则由垂径定理知,BN=AN=
解:连接MB、MA,过点M作MN⊥AB于点N;则由垂径定理知,BN=AN= AB;
AB;
∵点M的坐标为(1,2)、点A的坐标为(0,1),
∴MA=MB= ,MN=1,
,MN=1,
∴在直角三角形MBN中,BN=1(勾股定理),
∴AB=2BN=2,
∴yB=yA+2=3;
又∵点B在y轴上,
∴点B的坐标为:(0,3);
故答案是:(0,3).
点评:本题考查了垂径定理、勾股定理.解此类题目要注意将圆的问题转化成直角三角形的问题再进行计算.
分析:连接MB、MA,过点M作MN⊥AB于点N.根据垂径定理、勾股定理求得BN=AN=
 AB=1;然后由坐标与图形的性质求得点B的纵坐标.
AB=1;然后由坐标与图形的性质求得点B的纵坐标.解答:
 解:连接MB、MA,过点M作MN⊥AB于点N;则由垂径定理知,BN=AN=
解:连接MB、MA,过点M作MN⊥AB于点N;则由垂径定理知,BN=AN= AB;
AB;∵点M的坐标为(1,2)、点A的坐标为(0,1),
∴MA=MB=
 ,MN=1,
,MN=1,∴在直角三角形MBN中,BN=1(勾股定理),
∴AB=2BN=2,
∴yB=yA+2=3;
又∵点B在y轴上,
∴点B的坐标为:(0,3);
故答案是:(0,3).
点评:本题考查了垂径定理、勾股定理.解此类题目要注意将圆的问题转化成直角三角形的问题再进行计算.

练习册系列答案
相关题目
 如图,以点O′(1,1)为圆心,OO′为半径画圆,判断点P(-1,1),点Q(1,0),点R(2,2)和⊙O′的位置关系.
如图,以点O′(1,1)为圆心,OO′为半径画圆,判断点P(-1,1),点Q(1,0),点R(2,2)和⊙O′的位置关系. 26、如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A.EB与AD一定平行吗?为什么?
26、如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A.EB与AD一定平行吗?为什么? 12、如图,以点B为中心,把△ABC旋转180°.
12、如图,以点B为中心,把△ABC旋转180°. 如图,以点O为圆心的两个同心圆,当大圆的弦AB与小圆相切时弦长AB=8,则这两个同心圆所形成的圆环的面积是
如图,以点O为圆心的两个同心圆,当大圆的弦AB与小圆相切时弦长AB=8,则这两个同心圆所形成的圆环的面积是 如图,以点M(5,3)为圆心的⊙M切y轴于点A,与x轴交于B(1,0),C两点(点B在点C的左侧),直线l过圆心M且垂直于y轴,点P是直线l上的一个动点,如果△PAB的周长最小,那么此时点P的坐标是
如图,以点M(5,3)为圆心的⊙M切y轴于点A,与x轴交于B(1,0),C两点(点B在点C的左侧),直线l过圆心M且垂直于y轴,点P是直线l上的一个动点,如果△PAB的周长最小,那么此时点P的坐标是