题目内容
在边长为1的小正方形组成的方格纸中,若多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形。记格点多边形内的格点数为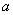 ,边界上的格点数为
,边界上的格点数为 ,则格点多边形的面积可表示为
,则格点多边形的面积可表示为 ,其中
,其中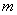 ,
, 为常数.
为常数.
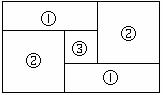
(1)在下面的方格纸中各画出一个面积为6的格点多边形,依次为三角形、平行四边形(非菱形)、菱形;
(2)利用(1)中的格点多边形确定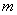 ,
, 的值.
的值.

解:(1)作图如下:

(2)三角形: ,
,
平行四边形(非菱形): ,
,
菱形: .
.
任选两组代入 ,如:
,如:
 ,解得
,解得 .
.
【考点】开放型;网格问题;图形的设计;待定系数法、方程思想和数形结合思想的应用.
【分析】(1)根据三角形、平行四边形(非菱形)、菱形的面积公式设计图形.
(2)应用待定系数法,根据三角形、平行四边形(非菱形)、菱形的 值代入
值代入 列方程组求解即可.
列方程组求解即可.

练习册系列答案
相关题目
 B.
B. C.
C. D.
D. 
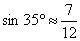 ,
, 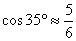 ,
,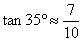
 ,并把解在数轴上表示出来.
,并把解在数轴上表示出来.
 ,则k的值是 ( )
,则k的值是 ( ) 的值为0,则
的值为0,则 的值为 .
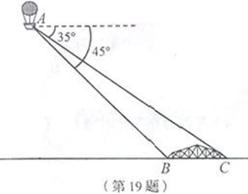
的值为 . ,观测渔船N在俯角
,观测渔船N在俯角 ,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米. .为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为
.为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为 ,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米? )
)