题目内容
16.(1)解方程:x2-4x+3=0.(2)计算:$\frac{{{a^2}-2a+1}}{{{a^2}-1}}-\frac{a}{a+1}$.
分析 (1)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
(2)根据公式法分解因式化简后进行同分母分式加减运算求出即可.
解答 解:(1)分解因式得:(x-3)(x-1)=0,
可得x-3=0或x-1=0,
解得:x1=3,x2=1(2)$-\frac{1}{a+1}$
(2)$\frac{{{a^2}-2a+1}}{{{a^2}-1}}-\frac{a}{a+1}$.
=$\frac{(a-1)^{2}}{(a-1)(a+1)}$-$\frac{a}{a+1}$
=$\frac{a-1}{a+1}$-$\frac{a}{a+1}$
=-$\frac{1}{a+1}$.
点评 此题考查了解一元二次方程-因式分解法和分式的运算,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
7.四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
| A. | AD=BC,AB=DC | B. | OA=OC,OB=OD | C. | AB∥DC,AD=BC | D. | ∠A=∠C,∠B=∠D |
5.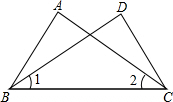 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )| A. | AB=CD | B. | AC=BD | C. | ∠A=∠D | D. | ∠ABC=∠DBC |
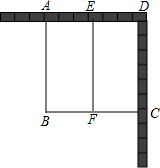 如图所示,某单位在两堵互相垂直的墙的墙角处,用可建60m长的建筑材料围成一个矩形堆物场地,中间用同样的材料EF分隔为两间,问AB为多长时,所围成的矩形面积是450m2?
如图所示,某单位在两堵互相垂直的墙的墙角处,用可建60m长的建筑材料围成一个矩形堆物场地,中间用同样的材料EF分隔为两间,问AB为多长时,所围成的矩形面积是450m2?