题目内容
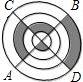
如图，AB，CD是⊙O的两条互相垂直的直径，点O1，O2，O3，O4分别是OA、OB、OC、OD的中点，若⊙O的半径为2，则阴影部分的面积为（ ）
A．8 B．4 C．4π+4 D．4π﹣4
考点：扇形面积的计算；圆与圆的位置关系．
分析：首先根据已知得出正方形内空白面积，进而得出扇形COB中两空白面积相等，进而得出阴影部分面积．
解答：解：如图所示：可得正方形EFMN，边长为2，
正方形中两部分阴影面积为：4﹣π，
∴正方形内空白面积为：4﹣2（4﹣π）=2π﹣4，
∵⊙O的半径为2，
∴O1，O2，O3，O4的半径为1，
∴小圆的面积为：π×12=π，
扇形COB的面积为：
=π，
∴扇形COB中两空白面积相等，
∴阴影部分的面积为：π×22﹣2（2π﹣4）=8．
故选：A．
点评：此题主要考查了扇形的面积公式以及正方形面积公式，根据已知得出空白面积是解题关键．
练习册系列答案
习题精选系列答案
相关题目
21、如图，AB、CD是⊙O的弦，∠A=∠C．求证：AB=CD．
如图，AB、CD是水平放置的轮盘（俯视图）上两条互相垂直的直径，一个小钢球在轮盘上自由滚动，该小钢球最终停在阴影区域的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2013•泰安）如图，AB，CD是⊙O的两条互相垂直的直径，点O1，O2，O3，O4分别是OA、OB、OC、OD的中点，若⊙O的半径为2，则阴影部分的面积为（ ）
（2013•盘锦）如图，AB，CD是⊙O的直径，点E在AB延长线上，FE⊥AB，BE=EF=2，FE的延长线交CD延长线于点G，DG=GE=3，连接FD．
如图，AB，CD是⊙O的两条弦，且AB=CD，点M是