题目内容
已知三角形的三边分别是15,20和25.则此三角形的最大边上的高是
- A.

- B.
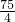
- C.9
- D.12
D
分析:根据三角形的三边的长,利用勾股定理逆定理求证该三角形为直角三角形,然后根据三角形面积公式得出 BD•AC=
BD•AC= AB•BC,即可求得答案.
AB•BC,即可求得答案.
解答: 解:已知三角形的三边分别是BC=15,AB=20,AC=25,BD是AC上的高,
解:已知三角形的三边分别是BC=15,AB=20,AC=25,BD是AC上的高,
∵BC=15,AB=20,AC=25,
∴AC2=AB2+BC2,
∴三角形ABC为直角三角形,
∵BD是AC上的高,
∴ BD•AC=
BD•AC= AB•BC,
AB•BC,
∴BD=12.
故选D.
点评:此题主要考查学生对三角形面积,和勾股定理逆定理的理解和掌握,解答此题的关键是根据三角形的三边的长,利用勾股定理逆定理求证该三角形为直角三角形.
分析:根据三角形的三边的长,利用勾股定理逆定理求证该三角形为直角三角形,然后根据三角形面积公式得出
 BD•AC=
BD•AC= AB•BC,即可求得答案.
AB•BC,即可求得答案.解答:
 解:已知三角形的三边分别是BC=15,AB=20,AC=25,BD是AC上的高,
解:已知三角形的三边分别是BC=15,AB=20,AC=25,BD是AC上的高,∵BC=15,AB=20,AC=25,
∴AC2=AB2+BC2,
∴三角形ABC为直角三角形,
∵BD是AC上的高,
∴
 BD•AC=
BD•AC= AB•BC,
AB•BC,∴BD=12.
故选D.
点评:此题主要考查学生对三角形面积,和勾股定理逆定理的理解和掌握,解答此题的关键是根据三角形的三边的长,利用勾股定理逆定理求证该三角形为直角三角形.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目