题目内容
小军从A地沿北偏西60°方向走10m到B地，再从B地向正南方向走20m到C地，此时小军离A地（ ）
A. 5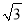
m B. 10m C. 15m D. 10
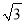m
D
【解析】试题分析：根据题意可得：A、B、C三点构成直角三角形，BC为斜边，则根据直角三角形的性质可得：AC=10m，故选D．
寒假乐园北京教育出版社系列答案如图，已知抛物线y=﹣x2+bx+c的对称轴为直线x=1，且与x轴的一个交点为（3，0），那么它对应的函数解析式是 ．
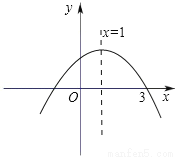
y=﹣x2+2x+3
【解析】
试题分析：∵抛物线y=﹣x2+bx+c的对称轴为直线x=1，
∴=1，解得b=2，
∵与x轴的一个交点为（3，0），
∴0=﹣9+6+c，
解得c=3，
故函数解析式为y=﹣x2+2x+3．
故答案为：y=﹣x2+2x+3 已知抛物线y＝ax2＋b x＋c经过A，B，C三点，当x≥0时，其图象如图所示．
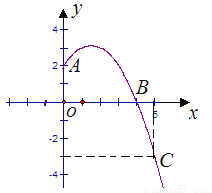
（1）求抛物线的解析式，写出抛物线的顶点坐标；
（2）画出抛物线y＝ax2＋b x＋c当x＜0时的图象；
（3）利用抛物线y＝ax2＋b x＋c，写出x为何值时，y＞0．
（1）抛物线y ＝顶点（，）（2）略（3） 当－1＜x＜4时， y >0
【解析】试题分析：本题的关键是求出抛物线的解析式，在题目给出的图象中可得出A、B、C三点的坐标，可用待定系数求出抛物线的解析式，进而可画出x＜0时抛物线的图象，以及y＞0时x的取值范围．
【解析】
（1）由图象，可知A（0，2），B（4，0），C（5，﹣3），
得方程组．
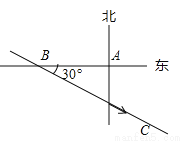
解得a=﹣，b=，c=2．... 温州市处于东南沿海，夏季经常遭受台风袭击．一次，温州气象局测得台风中心在温州市A的正西方向300千米的B处（如图），以每小时10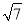
千米的速度向东偏南30°的BC方向移动，并检测到台风中心在移动过程中，温州市A将受到影响，且距台风中心200千米的范围是受台风严重影响的区域．则影响温州市A的时间会持续多长？（ ）
A. 5 B. 6 C. 8 D. 10
D
【解析】试题分析：过点A作AD⊥BC于D，由题意得AB=300，∠ABD＝30°，∴AD =150（km），
温州市点A受到台风严重影响设风台中心距A点200km处，刚好处在BC上的E，F两点
则在Rt△ADE中，AE＝200，AD＝150 ∴DE=50km， ∴EF=2DE=100km，
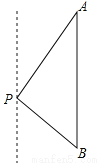
则t=100÷10=10h，故选D． 如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为（ ）
A. 40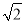
海里 B. 40
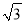海里 C. 80海里 D. 40
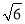海里
A
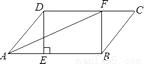
【解析】试题分析：过点P作PD⊥AB于点D，根据方位角可得：∠A=30°，∠B=45°，根据AP=80海里可得PD=40海里，PB=40海里，故选A． 在平行四边形ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．
（1）求证：四边形BFDE是矩形；
（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）根据平行四边形的性质，可得AB与CD的关系，根据平行四边形的判定，可得BFDE是平行四边形，再根据矩形的判定，可得答案；
（2）根据平行线的性质，可得∠DFA=∠FAB，根据等腰三角形的判定与性质，可得∠DAF=∠DFA，根据角平分线的判定，可得答案．
试题分析：（1）证明：∵四边形ABCD是平行四边形，
∴AB∥C... 平行四边形ABCD的周长32，5AB=3BC，则对角线AC的取值范围为（ ）
A．6＜AC＜10 B.6＜AC＜16 C.10＜AC＜16 D.4＜AC＜16
D．
【解析】
试题分析：∵平行四边形ABCD的周长32，5AB=3BC，∴2（AB+BC）=2（BC+BC）=32，
∴BC=10，∴AB=6，∴BC﹣AB＜AC＜BC+AB，即4＜AC＜16．
故选D． 已知x＝2时，分式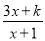
的值为零，则k＝__________.
-6
【解析】由题意得：6+k=0,解得：k=-6.
故答案：-6.