Question

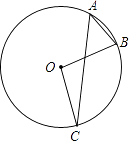
【题目】如图，直线和直线互相垂直，垂足为，直线于点B，E是线段AB上一定点，D为线段OB上的一动点（点D不与点O、B重合），直于点，连接AC．

（1）当，则___________°；

（2）当时，请判断CD与AC的位置关系，并说明理由；

（3）若、的角平分线的交点为P，当点D在线段上运动时，问的大小是否会发生变化？若不变，求出的大小，并说明理由；若变化，求其变化范围．

Answer 1

【答案】（1）40°；（2）AC⊥CD，理由见解析；（3）∠P=45°，理由见解析

【解析】

（1）首先根据题意得出∠EDB+∠BED=90°，∠CDO+∠EDB=90°，由此可以求出∠CDO度数，最后进一步求出答案即可；

（2）由（1）可得∠CDO=∠BED，然后进一步利用“同位角相等，两直线平行”证明CD∥AC，最后利用平行线性质进一步求证即可；

（3）连接PD并延长，首先根据角平分线性质得出∠1=∠OCD，∠2=∠BED，由此结合题意进一步得出∠1+∠2=45°，再根据三角形外角性质得出∠5=∠3∠1，∠6=∠4∠2，据此利用∠P=∠5+∠6进一步计算即可.

（1）∵直线，CD⊥DE，

∴∠EDB+∠BED=90°，∠CDO+∠EDB=90°，

∴∠CDO=∠BED=50°，

∵直线和直线互相垂直，

∴∠OCD=40°；

（2）由（1）可得：∠CDO=∠BED，

∵，

∴∠A=∠BED，

∴AC∥DE，

∵CD⊥DE，

∴AC⊥CD；

（3）∠P的大小不会发生变化，理由如下：

如图，连接PD并延长，

∵CP平分∠OCD，PE平分∠BED，

∴∠1=∠OCD，∠2=∠BED，

即∠1+∠2=(∠OCD+∠BED)，

∵∠CDO=∠BED，

∴∠OCD+∠BED=∠OCD+∠CDO=90°，

∴∠1+∠2=45°，

∵CD⊥DE，

∴∠3+∠4=90°，

∵∠5=∠3∠1，∠6=∠4∠2，

∴∠P=∠5+∠6=∠3∠1+∠4∠2=∠3+∠4(∠1+∠2)=45°，

即∠P的大小是定值45°.