题目内容
已知:直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.(1)填空:菱形ABCD的边长是______、面积是______、高BE的长是______;
(2)若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时,求△APQ的面积S关于t的函数关系式;
(3)若点P的速度为每秒1个单位,点Q的速度变为每秒k个单位,求出当t=4秒时,△APQ为等腰三角形时k的值.

【答案】分析:(1)求出OC=4,OD=3,在Rt△COD中,由勾股定理求出CD=5,求出AC=2OC=8,BD=2OD=6,即可求出菱形ABCD的面积( ×AC×BC),根据S=
×AC×BC),根据S= ×AC×BE,求出BE即可;
×AC×BE,求出BE即可;
(2)求出AP=t,AQ=10-2t,过点Q作QG⊥AD,垂足为G,根据△AQG∽△ABE求出QG= -
- t,代入S=
t,代入S= AP•QG求出即可;
AP•QG求出即可;
(3)当t=4秒时,求出AP=4,以下分两种情况讨论:第一种情况:当点Q在CB上时,只有Q1A=Q1P,过点Q1作Q1M⊥AP,垂足为点M,Q1M交AC于点F,根据△AMF∽△AOD∽△CQ1F求出FM= ,Q1F=
,Q1F= ,CQ1=
,CQ1= QF=
QF= ,由CQ1=4k,求出即可;第二种情况:当点Q在BA上时,存在两点Q2,Q3,分别使AP=AQ2,PA=PQ3.
,由CQ1=4k,求出即可;第二种情况:当点Q在BA上时,存在两点Q2,Q3,分别使AP=AQ2,PA=PQ3.
①若AP=AQ2,根据CB+BQ2=10-4=6得出4k=6,求出即可;
②若PA=PQ3,过点P作PN⊥AB,垂足为N,由△ANP∽△AEB,得 =
= ,求出AN=
,求出AN= ,AQ3=2AN=
,AQ3=2AN= ,求出BC+BQ3=
,求出BC+BQ3= ,由
,由 ,求出即可.
,求出即可.
解答:解:(1)∵C,D两点的坐标分别为(4,0),(0,3),
∴OC=4,OD=3,
在Rt△COD中,由勾股定理得:CD=5,
即菱形ABCD的边长是5,
∵四边形ABCD是菱形,
∴AD=DC=5,AC⊥BD,AC=2OC=8,BD=2OD=6,
∴菱形ABCD的面积是 ×AC×BC=
×AC×BC= ×6×8=24,
×6×8=24,
∴24= ×AC×BE,
×AC×BE,
∴BE= ;
;
(2)由题意,得AP=t,AQ=10-2t,
如图1,过点Q作QG⊥AD,垂足为G,由QG∥BE得:
△AQG∽△ABE,
∴ =
= ,
,
∴QG= -
- t,
t,
∴S= AP•QG=
AP•QG= •t•(
•t•( -
- t),
t),
S=- t2+
t2+ t;
t;
(3)当t=4秒时,
∵点P的速度为每秒1个单位,
∴AP=4,
以下分两种情况讨论:
第一种情况:当点Q在CB上时,
∵PQ≥BE>PA,∴只存在点Q1,使Q1A=Q1P,
如图2,过点Q1作Q1M⊥AP,垂足为点M,Q1M交AC于点F,
则AM= AP=2,
AP=2,
∵△AMF∽△AOD∽△CQ1F,
∴ =
= =
= =
= ,
,
∴FM= ,
,
∴Q1F=MQ1-FM= ,
,
∴CQ1= QF=
QF= ,
,
 由CQ1=4k,
由CQ1=4k,
∴k= ;
;
第二种情况:当点Q在BA上时,存在两点Q2,Q3,分别使AP=AQ2,PA=PQ3.
①若AP=AQ2,如图3,
CB+BQ2=10-4=6.由4k=6,得 ;
;
②若PA=PQ3,如图4,
过点P作PN⊥AB,垂足为N,
由△ANP∽△AEB,得 =
= ,
,
 ∵AE=
∵AE= =
= ,
,
∴AN= ,
,
∴AQ3=2AN= ,
,
∴BC+BQ3=10- =
= ,由
,由 ,
,
得 .
.
综上所述,当t=4秒,使得△APQ为等腰三角形的k的值为 或
或 或
或 .
.
故答案为:5,24, .
.
点评:本题考查了相似三角形的性质和判定,勾股定理,菱形性质的应用,主要考查学生综合运用性质进行推理和计算的能力,难度偏大,用了分类讨论思想.
 ×AC×BC),根据S=
×AC×BC),根据S= ×AC×BE,求出BE即可;
×AC×BE,求出BE即可;(2)求出AP=t,AQ=10-2t,过点Q作QG⊥AD,垂足为G,根据△AQG∽△ABE求出QG=
 -
- t,代入S=
t,代入S= AP•QG求出即可;
AP•QG求出即可;(3)当t=4秒时,求出AP=4,以下分两种情况讨论:第一种情况:当点Q在CB上时,只有Q1A=Q1P,过点Q1作Q1M⊥AP,垂足为点M,Q1M交AC于点F,根据△AMF∽△AOD∽△CQ1F求出FM=
 ,Q1F=
,Q1F= ,CQ1=
,CQ1= QF=
QF= ,由CQ1=4k,求出即可;第二种情况:当点Q在BA上时,存在两点Q2,Q3,分别使AP=AQ2,PA=PQ3.
,由CQ1=4k,求出即可;第二种情况:当点Q在BA上时,存在两点Q2,Q3,分别使AP=AQ2,PA=PQ3.①若AP=AQ2,根据CB+BQ2=10-4=6得出4k=6,求出即可;
②若PA=PQ3,过点P作PN⊥AB,垂足为N,由△ANP∽△AEB,得
 =
= ,求出AN=
,求出AN= ,AQ3=2AN=
,AQ3=2AN= ,求出BC+BQ3=
,求出BC+BQ3= ,由
,由 ,求出即可.
,求出即可.解答:解:(1)∵C,D两点的坐标分别为(4,0),(0,3),
∴OC=4,OD=3,
在Rt△COD中,由勾股定理得:CD=5,
即菱形ABCD的边长是5,
∵四边形ABCD是菱形,
∴AD=DC=5,AC⊥BD,AC=2OC=8,BD=2OD=6,
∴菱形ABCD的面积是
 ×AC×BC=
×AC×BC= ×6×8=24,
×6×8=24,∴24=
 ×AC×BE,
×AC×BE,∴BE=
 ;
;(2)由题意,得AP=t,AQ=10-2t,

如图1,过点Q作QG⊥AD,垂足为G,由QG∥BE得:
△AQG∽△ABE,
∴
 =
= ,
,∴QG=
 -
- t,
t,∴S=
 AP•QG=
AP•QG= •t•(
•t•( -
- t),
t),S=-
 t2+
t2+ t;
t;(3)当t=4秒时,
∵点P的速度为每秒1个单位,
∴AP=4,
以下分两种情况讨论:
第一种情况:当点Q在CB上时,

∵PQ≥BE>PA,∴只存在点Q1,使Q1A=Q1P,
如图2,过点Q1作Q1M⊥AP,垂足为点M,Q1M交AC于点F,
则AM=
 AP=2,
AP=2,∵△AMF∽△AOD∽△CQ1F,
∴
 =
= =
= =
= ,
,∴FM=
 ,
,∴Q1F=MQ1-FM=
 ,
,∴CQ1=
 QF=
QF= ,
, 由CQ1=4k,
由CQ1=4k,∴k=
 ;
;第二种情况:当点Q在BA上时,存在两点Q2,Q3,分别使AP=AQ2,PA=PQ3.
①若AP=AQ2,如图3,
CB+BQ2=10-4=6.由4k=6,得
 ;
;②若PA=PQ3,如图4,
过点P作PN⊥AB,垂足为N,
由△ANP∽△AEB,得
 =
= ,
, ∵AE=
∵AE= =
= ,
,∴AN=
 ,
,∴AQ3=2AN=
 ,
,∴BC+BQ3=10-
 =
= ,由
,由 ,
,得
 .
.综上所述,当t=4秒,使得△APQ为等腰三角形的k的值为
 或
或 或
或 .
.故答案为:5,24,
 .
.点评:本题考查了相似三角形的性质和判定,勾股定理,菱形性质的应用,主要考查学生综合运用性质进行推理和计算的能力,难度偏大,用了分类讨论思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
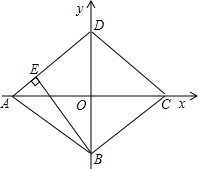 已知:直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.
已知:直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒. 已知平面直角坐标系中三点的坐标分别为:A(4、5),B(-2,2),C(3,0)
已知平面直角坐标系中三点的坐标分别为:A(4、5),B(-2,2),C(3,0)
