题目内容
8.写出大于-$\sqrt{7}$且小于$\sqrt{7}$的所有整数-2,-1,0,1,2.分析 先估算出$\sqrt{7}$的取值范围,进而可得出结论.
解答 解:∵4<7<9,
∴2<$\sqrt{7}$<3,
∴-3<-$\sqrt{7}$<-2,
∴大于-$\sqrt{7}$且小于$\sqrt{7}$的所有整数是-2,-1,0,1,2.
故答案为:-2,-1,0,1,2.
点评 本题考查的是估算无理数的大小,熟知估算无理数大小要用逼近法是解答此题的关键.

练习册系列答案
相关题目
18.等腰三角形的底角是70°,则顶角为( )
| A. | 40° | B. | 70° | C. | 55° | D. | 45° |
19.下列各组数中,不是x+y=5的解的是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=7}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=0}\\{y=5}\end{array}\right.$ |
3.下列实数是无理数的是( )
| A. | -1 | B. | 0 | C. | 3.14 | D. | $\sqrt{5}$ |
20.下列计算正确的是( )
| A. | $\sqrt{2}×\sqrt{\frac{1}{2}}$=1 | B. | $\sqrt{4}-\sqrt{3}=1$ | C. | $\sqrt{6}÷\sqrt{3}$=2 | D. | $\sqrt{8}=±\sqrt{2}$ |
17. 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM等于( )
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM等于( )
 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM等于( )
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM等于( )| A. | 5$\sqrt{3}$ | B. | 5$\sqrt{3}$-1 | C. | 5 | D. | 4 |
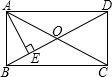 如图,矩形ABCD中,∠DAE:∠BAE=3:1,AE⊥BD,则∠EAC等于45°.
如图,矩形ABCD中,∠DAE:∠BAE=3:1,AE⊥BD,则∠EAC等于45°.