题目内容
已知△ABC中，AB=13cm，AC=20cm，第三边BC边上的高AD=12cm，则BC的长为 cm．
考点：勾股定理
专题：分类讨论
分析：分两种情况考虑，在直角三角形ACD与直角三角形ABD中，分别利用勾股定理求出CD与BD的长，由CD+DB及CD-BC分别求出BC的长即可．
解答：
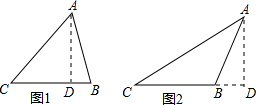解：如图1所示，在Rt△ACD中，AC=20cm，AD=12cm，
根据勾股定理得：CD=
=16cm，
在Rt△ABD中，AB=13cm，AD=12cm，
根据勾股定理得：BD=
=5cm，
此时BC=BD+DC=16+5=21cm；
如图2所示，在Rt△ACD中，AC=20cm，AD=12cm，
根据勾股定理得：CD=
=16cm，
在Rt△ABD中，AB=13cm，AD=12cm，
根据勾股定理得：BD=
=5cm，
此时BC=DC-BC=16-5=11cm，
综上，BC的长为11或21cm．
解：如图1所示，在Rt△ACD中，AC=20cm，AD=12cm，根据勾股定理得：CD=
| AC2-AD2 |
在Rt△ABD中，AB=13cm，AD=12cm，
根据勾股定理得：BD=
| AB2-AD2 |
此时BC=BD+DC=16+5=21cm；
如图2所示，在Rt△ACD中，AC=20cm，AD=12cm，
根据勾股定理得：CD=
| AC2-AD2 |
在Rt△ABD中，AB=13cm，AD=12cm，
根据勾股定理得：BD=
| AB2-AD2 |
此时BC=DC-BC=16-5=11cm，
综上，BC的长为11或21cm．
点评：此题考查了勾股定理，利用了分类讨论的思想，熟练掌握勾股定理是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知：如图，在△ABC中，BC∥x轴，点A的坐标是（-4，3），点B的坐标是（-3，1）
如图，△ABC内接于⊙O，OD⊥BC于点D，∠A=55°，则∠OCD的度数是
用5个大小相同的小长方形拼成了如图所示的大长方形，若大长方形的周长是14，则每个小长方形的周长是在矩形ABCD中，E，F分别为AB，CD的中点，如果矩形ABCD∽矩形EFCB，那么它们的相似比为（ ）
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|