题目内容
5. 如图,折叠矩形纸片ABCD,使B点落在AD上的点E处,折痕的端点分别在AB,BC上(含端点),AB=6,BC=10,求AE的取值范围.
如图,折叠矩形纸片ABCD,使B点落在AD上的点E处,折痕的端点分别在AB,BC上(含端点),AB=6,BC=10,求AE的取值范围.
分析 设折痕为PQ,点P在AB边上,点Q在BC边上.分别利用当点P与点A重合时,以及当点Q与点C重合时,求出AE的极值进而得出答案.
解答 解:设折痕为PQ,点P在AB边上,点Q在BC边上.
如图1,当点Q与点C重合时,根据翻折对称性可得
EC=BC=10,
在Rt△CDE中,CE2=CD2+ED2,
即102=(10-AE)2+62,
解得:AE=2,
如图2,当点P与点A重合时,根据翻折对称性可得
AE=AB=6,
所以,AE的取值范围是2≤x≤6.
点评 本题考查的是翻折变换(折叠问题)、勾股定理.注意利用翻折变换的性质得出对应线段之间的关系是解题关键.

练习册系列答案
相关题目
14.如果a+b=2,那么a2+2ab+b2的值是( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
15.下列计算中,正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | a9÷a3=a3 | D. | (-a3)2=a6 |
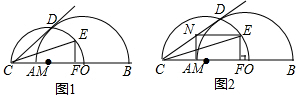
 如图,图中共有6 条线段,7 个小于平角的角.
如图,图中共有6 条线段,7 个小于平角的角. 如图所示,点B在点A南偏东39°方向.
如图所示,点B在点A南偏东39°方向.