题目内容
10.复习课中,教师给出关于x的函数y=-2k2x-1+k2(k≠0).同学们在独立思考后,探索并写出了与该函数有关的许多结论(性质),教师也补充了几条结论,现从中选出以下四条:①此函数是一次函数,但不可能是正比例函数;
②此函数图象必通过第二、四象限,且函数值y随着自变量x的增大而减小;
③若函数图象与x轴交于点A(a,0),则a<0.5;
④此函数图象与直线y=4x-3、y轴围成的三角形的面积必小于0.5
教师:请你分别判断四条结论的真假,并给出理由.最后总结回顾并简单写出解决以上问题时所用的数学思想方法.
分析 ①通过反例即可判断;
②根据一次函数的性质即可判断;
③先利用函数值为0可计算出a=$\frac{1}{2}$-$\frac{1}{2{k}^{2}}$,则$\frac{1}{2{k}^{2}}$>0,a<0.5,于是可进行判断;
④求出直线y=-2k2x-1+k2(k≠0)和直线y=4x-3的交点坐标,以及它们与y轴的交点坐标,则根据三角形面积公式得到直线y=-2k2x-1+k2与直线y=4x-3、y轴围成的面积为$\frac{1}{4}$k2+$\frac{1}{2}$>0.5,即可进行判断.
解答 解:此函数是一次函数,当k=±1时,它是正比例函数,所以①是假命题;
∵-2k2<0,∴此函数图象必通过第二、四象限,且函数值y随着自变量x的增大而减小,所以②真命题;
若函数图象与x轴交于A(a,0),令y=0,则-2k2x-1+k2=0,解得x=$\frac{{k}^{2}-1}{2{k}^{2}}$=$\frac{1}{2}$-$\frac{1}{2{k}^{2}}$,∵$\frac{1}{2{k}^{2}}$>0时,∴a<0.5,所以③是真命题;
此函数图象与直线y=4x-3的交点坐标为($\frac{1}{2}$,-1),此直线与y轴的交点坐标为(0,-1+k2),直线y=4x-3与y轴的交点坐标为(0,-3),所以此函数图象与直线y=4x-3、y轴围成的面积=$\frac{1}{2}$•|-1+k2+3|•$\frac{1}{2}$=$\frac{1}{4}$•(k2+2)=$\frac{1}{4}$k2+$\frac{1}{2}$>0.5,所以④是假命题.
点评 本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.

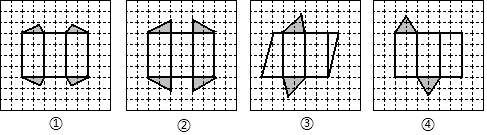
| A. | ①和④ | B. | ③和④ | C. | ①和② | D. | ②③④ |
 如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是4cm2,则它移动的距离AA′等于( )
如图,将边长为4cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积是4cm2,则它移动的距离AA′等于( )| A. | 3cm | B. | 2.5cm | C. | 1.5cm | D. | 2cm |
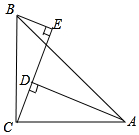 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D
 如图,折叠矩形纸片ABCD,使B点落在AD上的点E处,折痕的端点分别在AB,BC上(含端点),AB=6,BC=10,求AE的取值范围.
如图,折叠矩形纸片ABCD,使B点落在AD上的点E处,折痕的端点分别在AB,BC上(含端点),AB=6,BC=10,求AE的取值范围.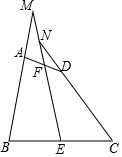 如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.
如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE. 如图,已知AB=AC,DB=DC,F是AD的延长线上一点,求证:∠ABF=∠ACF.
如图,已知AB=AC,DB=DC,F是AD的延长线上一点,求证:∠ABF=∠ACF.