题目内容
已知抛物线y=ax2+bx+c（a≠0）经过点（1，1）和（-1，0）．下列结论：
①a-b+c=0；
②b2＞4ac；
③当a＜0时，抛物线与x轴必有一个交点在点（1，0）的右侧；
④抛物线的对称轴为x=-
．
其中结论正确的个数有（ ）
①a-b+c=0；
②b2＞4ac；
③当a＜0时，抛物线与x轴必有一个交点在点（1，0）的右侧；
④抛物线的对称轴为x=-
| 1 |
| 4a |
其中结论正确的个数有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知反比例函数y=
下列关于抛物线y=
x2和y=-
x2的关系说法中，正确的是 （ ）
| 1 |
| 3 |
| 1 |
| 3 |
| A、它们的形状相同，开口也相同 | ||||
| B、它们都关于y轴对称 | ||||
| C、它们的顶点不相同 | ||||
D、点（-3，3）既在抛物线y=
|
二次函数y=-x2+bx+c的图象如图，下列几个结论：①对称轴为x=2；
②当y≤0时，x＜0或x＞4；
③函数解析式为y=-x（x-4）；
④当x≤0时，y随x的增大而增大．
其中正确的结论有（ ）
| A、①②③④ | B、①②③ | C、②③④ | D、①③④ |
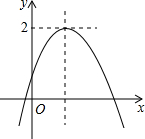已知二次函数y=ax2+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论：①b2-4ac＞0；②abc＜0；③m＞2．
其中，正确结论的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
二次函数y=ax2+bx+c（a≠0）的部分图象如图，图象过点（-1，0），对称轴为直线x=2，下列结论：①4a+b=0；②9a+c＞3b；③8a+7b+2c＞0；④当x＞-1时，y的值随x值的增大而增大．
其中正确的结论有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
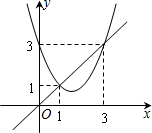函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2-4c＜0；②c-b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b-1）x+c＜0．
其中正确结论的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
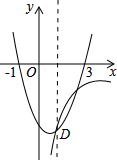如图，在平面直角坐标系内，二次函数y=ax2+bx+c（a≠0）的图象的顶点D在第四象限内，且该图象与x轴的两个交点的横坐标分别为-1和3．若反比例函数y=| k |
| x |
| A、b=-2a |
| B、a+b+c＜0 |
| C、c=a+k |
| D、a+2b+4c＜8k |
把抛物线y=x2+1向左平移l个单位，然后向上平移3个单位，则平移后抛物线的解折式为（ ）
| A、y=（x+3）2+1 | B、y=（x+1）2+3 | C、y=（x-1）2+4 | D、y=（x+1）2+4 |