题目内容
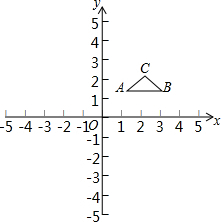 如图△ABC在平面直角坐标系内,它的三个顶点的坐标分别为A(1,
如图△ABC在平面直角坐标系内,它的三个顶点的坐标分别为A(1, ),B(3,
),B(3, ),C(2,
),C(2, ).
).
(1)若将△ABC向下平移 个单位长度,求所得三角形的三个顶点的坐标.
个单位长度,求所得三角形的三个顶点的坐标.
(2)求△ABC的面积.
解:(1)∵△ABC向下平移 个单位长度,
个单位长度,
∴点A、B的纵坐标为, -
- =0,
=0,
点C的纵坐标 -
- ,
,
∴A(1,0),B(3,0),C(2, -
- );
);
(2)∵A(1, ),B(3,
),B(3, ),C(2,
),C(2, ),
),
∴AB=3-1=2,点C到AB的距离为 -
- ,
,
∴△ABC的面积= ×2×(
×2×( -
- )=
)= -
- .
.
分析:(1)根据向下平移,横坐标不变,纵坐标减,求出点A、B、C的纵坐标即可得解;
(2)根据点A、B、C的坐标求出AB的长度,再求出点C到AB的距离,然后利用三角形的面积公式列式计算即可得解.
点评:本题考查了坐标与图形的性质-平移,熟记平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.
 个单位长度,
个单位长度,∴点A、B的纵坐标为,
 -
- =0,
=0,点C的纵坐标
 -
- ,
,∴A(1,0),B(3,0),C(2,
 -
- );
);(2)∵A(1,
 ),B(3,
),B(3, ),C(2,
),C(2, ),
),∴AB=3-1=2,点C到AB的距离为
 -
- ,
,∴△ABC的面积=
 ×2×(
×2×( -
- )=
)= -
- .
.分析:(1)根据向下平移,横坐标不变,纵坐标减,求出点A、B、C的纵坐标即可得解;
(2)根据点A、B、C的坐标求出AB的长度,再求出点C到AB的距离,然后利用三角形的面积公式列式计算即可得解.
点评:本题考查了坐标与图形的性质-平移,熟记平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目

 .△FED不动,△ABC沿直线BE以每秒1个单位的速度向右平移,直到点B与点E重合为止,设移动x秒后两个三角形重叠部分的面积为s.
.△FED不动,△ABC沿直线BE以每秒1个单位的速度向右平移,直到点B与点E重合为止,设移动x秒后两个三角形重叠部分的面积为s.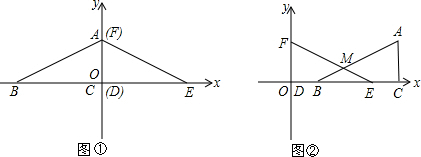
 ),求出过F、M、A三点的抛物线的解析式;此抛物线上有一动点P,以点P为圆心,以2为半径的⊙P在运动过程中是否存在与y轴相切的情况?若存在,直接写出P点的坐标;若不存在,请说明理由.
),求出过F、M、A三点的抛物线的解析式;此抛物线上有一动点P,以点P为圆心,以2为半径的⊙P在运动过程中是否存在与y轴相切的情况?若存在,直接写出P点的坐标;若不存在,请说明理由. .△FED不动,△ABC沿直线BE以每秒1个单位的速度向右平移,直到点B与点E重合为止,设移动x秒后两个三角形重叠部分的面积为s.
.△FED不动,△ABC沿直线BE以每秒1个单位的速度向右平移,直到点B与点E重合为止,设移动x秒后两个三角形重叠部分的面积为s.
 ),求出过F、M、A三点的抛物线的解析式;此抛物线上有一动点P,以点P为圆心,以2为半径的⊙P在运动过程中是否存在与y轴相切的情况?若存在,直接写出P点的坐标;若不存在,请说明理由.
),求出过F、M、A三点的抛物线的解析式;此抛物线上有一动点P,以点P为圆心,以2为半径的⊙P在运动过程中是否存在与y轴相切的情况?若存在,直接写出P点的坐标;若不存在,请说明理由. .△FED不动,△ABC沿直线BE以每秒1个单位的速度向右平移,直到点B与点E重合为止,设移动x秒后两个三角形重叠部分的面积为s.
.△FED不动,△ABC沿直线BE以每秒1个单位的速度向右平移,直到点B与点E重合为止,设移动x秒后两个三角形重叠部分的面积为s.
 ),求出过F、M、A三点的抛物线的解析式;此抛物线上有一动点P,以点P为圆心,以2为半径的⊙P在运动过程中是否存在与y轴相切的情况?若存在,直接写出P点的坐标;若不存在,请说明理由.
),求出过F、M、A三点的抛物线的解析式;此抛物线上有一动点P,以点P为圆心,以2为半径的⊙P在运动过程中是否存在与y轴相切的情况?若存在,直接写出P点的坐标;若不存在,请说明理由.