题目内容
(2012•呼伦贝尔)如图①,在平面直角坐标系内,Rt△ABC≌Rt△FED,点C、D与原点O重合,点A、F在y轴上重合,∠B=∠E=30°,AC=FD=
.△FED不动,△ABC沿直线BE以每秒1个单位的速度向右平移,直到点B与点E重合为止,设移动x秒后两个三角形重叠部分的面积为s.

(1)求出图①中点B的坐标;
(2)如图②,当x=4秒时,点M坐标为(2,
),求出过F、M、A三点的抛物线的解析式;此抛物线上有一动点P,以点P为圆心,以2为半径的⊙P在运动过程中是否存在与y轴相切的情况?若存在,直接写出P点的坐标;若不存在,请说明理由.
(3)求出整个运动过程中s与x的函数关系式.
| 3 |

(1)求出图①中点B的坐标;
(2)如图②,当x=4秒时,点M坐标为(2,
| ||
| 3 |
(3)求出整个运动过程中s与x的函数关系式.
分析:(1)求图①中点B的坐标,就需要求出线段BC的长,在Rt△ABC中,已知AC的长以及∠B的度数,由∠B的正弦函数即可求出BC的长;
(2)首先需要求点A的坐标,依题意,点A向右平移了4个单位,那么点A的坐标易知,而点F、M坐标已知,利用待定系数法确定抛物线的解析式;在求点P的坐标时,需要注意⊙P与y轴相切的条件,⊙P的半径为2,那么点P的横坐标必为±2,代入前面求得的抛物线解析式中,即可得到点P的坐标;
(3)此题需要分作两个阶段考虑:
①当点B在点O左侧时,两个三角形的重叠部分是五边形,那么它的面积可由直角梯形的面积减去左上角的小三角形的面积求得;
②当点B运动到线段DE上时,两个三角形的重叠部分是等腰三角形,BE的长易知,而BE边上的高为
×
BE,则面积易得.
(2)首先需要求点A的坐标,依题意,点A向右平移了4个单位,那么点A的坐标易知,而点F、M坐标已知,利用待定系数法确定抛物线的解析式;在求点P的坐标时,需要注意⊙P与y轴相切的条件,⊙P的半径为2,那么点P的横坐标必为±2,代入前面求得的抛物线解析式中,即可得到点P的坐标;
(3)此题需要分作两个阶段考虑:
①当点B在点O左侧时,两个三角形的重叠部分是五边形,那么它的面积可由直角梯形的面积减去左上角的小三角形的面积求得;
②当点B运动到线段DE上时,两个三角形的重叠部分是等腰三角形,BE的长易知,而BE边上的高为
| ||
| 3 |
| 1 |
| 2 |
解答: 解:(1)如图①,在Rt△ABC中,AC=
解:(1)如图①,在Rt△ABC中,AC=
,∠B=30°;
∴BC=
AC=3,即 B(-3,0);
(2)如图②,∵x=4,∴A(4,
);
设抛物线的解析式为:y=ax2+bx+c,依题意,有:
,
解得
,
∴抛物线的解析式:y=
x2-
x+
.
若半径为2的⊙P与y轴相切,那么点P的横坐标为2或-2;
当x=2时,y=
x2-
x+
=
;
当x=-2时,y=
x2-
x+
=3
;
∴存在符合条件的点P,且坐标为(2,
)或(-2,3
);
 (3)当点B、O重合时,x=3,所以整个过程可分作两个阶段:
(3)当点B、O重合时,x=3,所以整个过程可分作两个阶段:
①0≤x<3时,如图①;
BO=3-x,CD=x,OG=CH=
BO=
(3-x),FG=
-
(3-x)=
x;
∴s=S梯形FDCH-S△FGM
=
×(
+
-
x)×x-
×
x×
x
=-
x2+
x;
②3≤x≤6时,如图②,BE=6-x;
s=S△BME=
×(6-x)×(
×
)=
x2-
x+3
;
综上,s=
.
 解:(1)如图①,在Rt△ABC中,AC=
解:(1)如图①,在Rt△ABC中,AC=| 3 |
∴BC=
| 3 |
(2)如图②,∵x=4,∴A(4,
| 3 |
设抛物线的解析式为:y=ax2+bx+c,依题意,有:
|
解得
|
∴抛物线的解析式:y=
| ||
| 6 |
2
| ||
| 3 |
| 3 |
若半径为2的⊙P与y轴相切,那么点P的横坐标为2或-2;
当x=2时,y=
| ||
| 6 |
2
| ||
| 3 |
| 3 |
| ||
| 3 |
当x=-2时,y=
| ||
| 6 |
2
| ||
| 3 |
| 3 |
| 3 |
∴存在符合条件的点P,且坐标为(2,
| ||
| 3 |
| 3 |
 (3)当点B、O重合时,x=3,所以整个过程可分作两个阶段:
(3)当点B、O重合时,x=3,所以整个过程可分作两个阶段:①0≤x<3时,如图①;
BO=3-x,CD=x,OG=CH=
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
∴s=S梯形FDCH-S△FGM
=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
=-
| ||
| 4 |
| 3 |
②3≤x≤6时,如图②,BE=6-x;
s=S△BME=
| 1 |
| 2 |
| 6-x |
| 2 |
| ||
| 3 |
| ||
| 12 |
| 3 |
| 3 |
综上,s=
|
点评:此题主要考查了函数解析式的确定、解直角三角形、直线与圆的位置关系以及图形面积的求法等综合知识;最后一题中,要注意抓住图形平移过程中的关键位置,据此来对函数进行分段,以便做到不重不漏.

练习册系列答案
相关题目
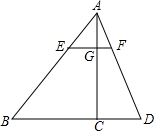 (2012•呼伦贝尔)如图,△ABD中,EF∥BD交AB于点E、交AD于点F,AC交EF于点G、交BD于点C,S△AEG=
(2012•呼伦贝尔)如图,△ABD中,EF∥BD交AB于点E、交AD于点F,AC交EF于点G、交BD于点C,S△AEG=