题目内容
6.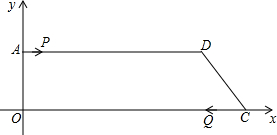 在平面直角坐标系中,O为坐标原点,坐标轴上两点A、C的坐标分别为(0,8),(32,0),AD∥OC,DC=8$\sqrt{2}$,点P从A出发,以每秒1个单位的速度沿着AD向D点运动;点Q从C点同时出发,以每秒3个单位的速度沿着CO向左运动,当点P到达D点时,点P、Q同时停止运动,设点P的运动时间为t秒.
在平面直角坐标系中,O为坐标原点,坐标轴上两点A、C的坐标分别为(0,8),(32,0),AD∥OC,DC=8$\sqrt{2}$,点P从A出发,以每秒1个单位的速度沿着AD向D点运动;点Q从C点同时出发,以每秒3个单位的速度沿着CO向左运动,当点P到达D点时,点P、Q同时停止运动,设点P的运动时间为t秒.(1)图中线段AD的长度为24,当t=6时,四边形PQCD是平行四边形
(2)从运动开始,是否存在某个t值,使得以P、D、O、Q为顶点的四边形是平行四边形?若存在,求出t值;若不存在,说明理由.
(3)从运动开始,是否存在某个t值,使得四边形AOQP恰好为正方形?若存在,求出t值;若不存在,说明理由.
分析 (1)作DB⊥OC交OC于点B,由A、C的坐标,可得DB的值,利用勾股定理可得BC的值,由当PD=CQ时,四边形PQCD是平行四边形,可列出24-t=3t,求出t的值即可;
(2)分两种情况:①当PO=DQ时,四边形PDQO是平行四边形,②)当PO=DQ时,四边形PDOQ是平行四边形时分别求解即可;
(3)由四边形AOQP恰好为正方形,可得AP=AO=8,此时t=8,可求出OQ=8,即可得出当t=8时,四边形AOQP恰好为正方形.
解答 解:(1)如图1,作DB⊥OC交OC于点B,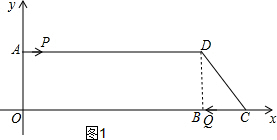
∵A、C的坐标分别为(0,8),(32,0),
∴DB=AO=8,DC=8$\sqrt{2}$,
∴BC=$\sqrt{D{C}^{2}-D{B}^{2}}$=$\sqrt{128-64}$=8,
∴AD=OC-OB=32-8=24,
∵当PD=CQ时,四边形PQCD是平行四边形,
∴24-t=3t,解得t=6,
∴当t=6时,四边形PQCD是平行四边形,
故答案为:24,6.
(2)存在.
①∵当PO=DQ时,四边形PDQO是平行四边形,
∴24-t=32-3t,解得t=4,
∴当t=4时,四边形PDQO是平行四边形,
②)∵当PO=DQ时,四边形PDOQ是平行四边形,
∴24-t=3t-32,解得t=14,
∴当t=14时,四边形PDOQ是平行四边形,
(3)存在.
∵四边形AOQP恰好为正方形,
∴AP=AO=8,此时t=8,
∴OQ=32-3×8=8,
∴当t=8时,四边形AOQP恰好为正方形.
点评 本题主要考查了四边形的综合题,涉及勾股定理,平行四边形的性质及正方形的判定,解题的关键是分类讨论.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
17.点P(3,-5)到x轴、y轴的距离分别是( )
| A. | 3,5 | B. | 5,3 | C. | -5,3 | D. | -3,5 |
14.一个角的余角比它的补角的$\frac{1}{3}$大10°,则这个角等于( )
| A. | 20° | B. | 30° | C. | 60° | D. | 70° |
18.下列各点中,在反比例函数y=-$\frac{3}{x}$图象上,但不在一次函数y=-2x+1图象上的点是( )
| A. | (-1,3) | B. | ($\frac{3}{2}$,-2) | C. | (-$\frac{3}{2}$,2) | D. | (-2,5) |
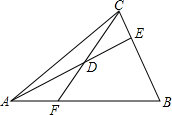 如图,△ABC中,CF与AE交于点D.
如图,△ABC中,CF与AE交于点D.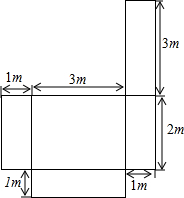 如图是一张铁片.
如图是一张铁片.