题目内容
2(3+1)(32+1)(34+1)(38+1)(316+1)(332+1)+1的个位数字为( )
| A、1 | B、3 | C、7 | D、9 |
考点:平方差公式,尾数特征
专题:计算题
分析:原式中2变形为(3-1)后,利用平方差公式计算即可得到结果.
解答:解:原式=(3-1)(3+1)(32+1)(34+1)(38+1)(316+1)(332+1)+1
=(32-1)(32+1)(34+1)(38+1)(316+1)(332+1)+1
=(34-1)(34+1)(38+1)(316+1)(332+1)+1
=(38-1)(38+1)(316+1)(332+1)+1
=(316-1)(316+1)(332+1)+1
=(332-1)(332+1)+1
=364-1+1
=364,
则结果的个位数字为1.
故选A
=(32-1)(32+1)(34+1)(38+1)(316+1)(332+1)+1
=(34-1)(34+1)(38+1)(316+1)(332+1)+1
=(38-1)(38+1)(316+1)(332+1)+1
=(316-1)(316+1)(332+1)+1
=(332-1)(332+1)+1
=364-1+1
=364,
则结果的个位数字为1.
故选A
点评:此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各式的计算中不正确的个数是( )
(1)100÷10-1=10;
(2)10-4•(2×7)0=1000;
(3)(0.1)0÷(-
)-3=8;
(4)(-10)-4÷(-
)-4=-1.
(1)100÷10-1=10;
(2)10-4•(2×7)0=1000;
(3)(0.1)0÷(-
| 1 |
| 2 |
(4)(-10)-4÷(-
| 1 |
| 10 |
| A、4个 | B、3个 | C、2个 | D、1个 |
下列运算中,错误的运算有( )
①(2x+y)2=4x2+y2,②(a-3b)2=a2-9b2,③(-x-y)2=x2-2xy+y2,④(x-
)2=x2-2x+
.
①(2x+y)2=4x2+y2,②(a-3b)2=a2-9b2,③(-x-y)2=x2-2xy+y2,④(x-
| 1 |
| 2 |
| 1 |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是( )


| A、①② | B、②③ | C、②④ | D、③④ |
若二次根式
在实数范围内有意义,则x的取值范围是( )
| ||
| 2x+1 |
| A、x≥-1 | ||
B、x≠-
| ||
C、x≥-1且x≠-
| ||
| D、以上都不正确 |
已知9x2+kxy+4y2是一个完全平方展开式,那么k的值是( )
| A、12 | B、24 |
| C、±12 | D、±24 |
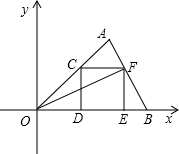 如图,在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
如图,在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.