题目内容
如图，已知∠BDE与∠B互补，∠1=30°，∠2=55°，则∠DEC的度数是
- A.85°
- B.105°
- C.95°
- D.125°
C
分析：根据平行线的判定与性质即可得出DE∥BC，再根据余角与补角即可求解；
解答：∵∠BDE与∠B互补，
∴DE∥BC，
∴∠BCE+∠CED=180°，
∵∠1=30°，∠2=55°，
∴∠DEC=180°-30°-55°=95°．
故选C．
点评：本题考查了平行线的判定与性质及余角与补角，属于基础题，关键是正确利用平行线的判定与性质．
分析：根据平行线的判定与性质即可得出DE∥BC，再根据余角与补角即可求解；
解答：∵∠BDE与∠B互补，
∴DE∥BC，
∴∠BCE+∠CED=180°，
∵∠1=30°，∠2=55°，
∴∠DEC=180°-30°-55°=95°．
故选C．
点评：本题考查了平行线的判定与性质及余角与补角，属于基础题，关键是正确利用平行线的判定与性质．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
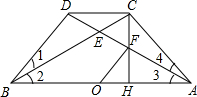如图，已知AD与BC相交于E，∠1=∠2=∠3，BD=CD，∠ADB=90°，CH⊥AB于H，CH交AD于F．
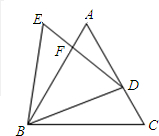如图，已知△ABC与△BDE都是等边三角形，点D在边AC上（不与A、C重合），DE与AB相交于点F．