题目内容
10.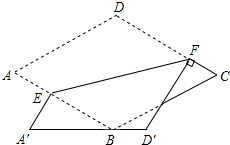 如图,菱形ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{FD}$的值为$\frac{\sqrt{3}-1}{2}$.
如图,菱形ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{FD}$的值为$\frac{\sqrt{3}-1}{2}$.
分析 设BC与D′F交于点K.CF=a,D′K=b,用a、b表示CK,KF,BK,根据BC=CD列出方程即可证明a=b,由此即可解决问题.
解答 解:设BC与D′F交于点K.CF=a,D′K=b,
∵四边形ABCD是菱形,∠A=60°,
∴∠C=60°,∠D′=∠D=120°,
∵KF⊥CD,
∴∠KFC=90°,
∴∠FKC=∠BKD′=30°,
∴∠KBD′=180°-∠D′-∠BKD′=30°,
∴BD′=b,BK=$\sqrt{3}$b,KC=2a,KF=$\sqrt{3}$a,
∵BC=CD=D′F+CF,
∴$\sqrt{3}$b+2a=b+$\sqrt{3}$a+a,
∴($\sqrt{3}$-1)a=($\sqrt{3}$-1)b,
∴a=b,
∴$\frac{CF}{DF}$=$\frac{a}{\sqrt{3}a+a}$=$\frac{\sqrt{3}-1}{2}$,
故答案为$\frac{\sqrt{3}-1}{2}$.
点评 本题考查菱形的性质、翻折变换、直角三角形30度角性质等知识,解题的关键是设参数,列出方程找到a、b的关系,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.在糖水中继续放入糖x(g)、水y(g),并使糖完全溶解,如果甜度保持不变,那么y与x的函数关系一定是( )
| A. | 正比例函数 | B. | 反比例函数 | ||
| C. | 图象不经过原点的一次函数 | D. | 二次函数 |
18. 如图,数轴上的A、B、C、D四点中,与表示数-$\sqrt{5}$的点最接近的是( )
如图,数轴上的A、B、C、D四点中,与表示数-$\sqrt{5}$的点最接近的是( )
 如图,数轴上的A、B、C、D四点中,与表示数-$\sqrt{5}$的点最接近的是( )
如图,数轴上的A、B、C、D四点中,与表示数-$\sqrt{5}$的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
5.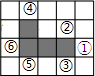 如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
 如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
20.中共中央、国务院近日印发的《国家创新驱动发展战略纲要》强调,要增强企业创新能力,发展壮大创新型企业家群体,推动创新创业,激发全社会创造活力.据悉,2015年全社会研发资金达14 000多亿元.将14 000用科学记数法表示应为( )
| A. | 0.14×105 | B. | 1.4×104 | C. | 1.4×105 | D. | 0.14×106 |

