题目内容
8. 如图,已知Rt△ABC≌Rt△DEC,连结AD,若∠1=20°,则∠B的度数是65°.
如图,已知Rt△ABC≌Rt△DEC,连结AD,若∠1=20°,则∠B的度数是65°.
分析 根据Rt△ABC≌Rt△DEC得出AC=CD,然后判断出△ACD是等腰直角三角形,根据等腰直角三角形的性质可得∠CAD=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠DEC,然后根据全等三角形的性质可得∠B=∠DEC.
解答 解:∵Rt△ABC≌Rt△DEC,
∴AC=CD,
∴△ACD是等腰直角三角形,
∴∠CAD=45°,
∴∠DEC=∠1+∠CAD=20°+45°=65°,
由Rt△ABC≌Rt△DEC的性质得∠B=∠DEC=65°.
故答案为:65°.
点评 本题考查了全等三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
3.某商场一天中售出李宁运动鞋11双,其中各种尺码的鞋的销售量如下表所示,
那么这11双鞋的尺码组成的一组数据中,众数与中位数分别为( )
| 鞋的尺码(单位:cm) | 23.5 | 24 | 24.5 | 25 | 26 |
| 销售量(单位:双) | 1 | 2 | 2 | 5 | 1 |
| A. | 25,24.5 | B. | 24.5,25 | C. | 26,25 | D. | 25,25 |
13.在平面直角坐标系中,点P(2,-1)关于y轴对称的点Q的坐标为( )
| A. | (-2,-1) | B. | (-2,1) | C. | (2,1) | D. | (1,-2) |
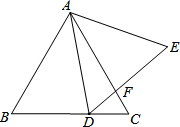 如图,已知:△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC交于点F
如图,已知:△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC交于点F 如图,直线y=-3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=$\frac{k}{x}$(k≠0)上的点D1处,则a=2.
如图,直线y=-3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=$\frac{k}{x}$(k≠0)上的点D1处,则a=2. 如图,在四边形ABCO中,点A与点C关于x轴对称,点B的坐标为(2,0),点C的坐标为(1,2),求点A的坐标及对角线OB,AC的长.
如图,在四边形ABCO中,点A与点C关于x轴对称,点B的坐标为(2,0),点C的坐标为(1,2),求点A的坐标及对角线OB,AC的长.