题目内容
如图,抛物线y=x2+bx+c与直线y=x﹣1交于A、B两点.点A的横坐标为﹣3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时,S四边形OBDC=2S△BPD;
(3)是否存在点P,使△PAD是直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
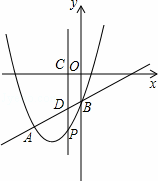
解:(1)∵y=x﹣1,∴x=0时,y=﹣1,∴B(0,﹣1).
当x=﹣3时,y=﹣4,∴A(﹣3,﹣4).
∵y=x2+bx+c与直线y=x﹣1交于A、B两点,∴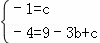 ,∴
,∴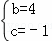 ,
,
∴抛物线的解析式为:y=x2+4x﹣1;
(2)∵P点横坐标是m(m<0),∴P(m,m2+4m﹣1),D(m,m﹣1)
如图1①,作BE⊥PC于E,
∴BE=﹣m.
CD=1﹣m,OB=1,OC=﹣m,CP=1﹣4m﹣m2,
∴PD=1﹣4m﹣m2﹣1+m=﹣3m﹣m2,
∴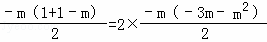 ,
,
解得:m1=0(舍去),m2=﹣2,m3=﹣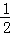 ;
;
如图1②,作BE⊥PC于E,
∴BE=﹣m.
PD=1﹣4m﹣m2+1﹣m=2﹣4m﹣m2,
∴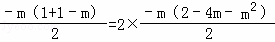 ,
,
解得:m=0(舍去)或m=﹣3,
∴m=﹣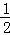 ,﹣2或﹣3时S四边形OBDC=2S△BPD;
,﹣2或﹣3时S四边形OBDC=2S△BPD;
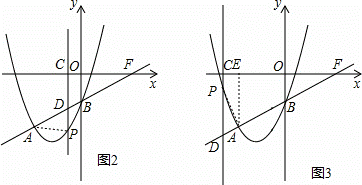
(3))如图2,当∠APD=90°时,设P(a,a2+4a﹣1),则D(a,a﹣1),
∴AP=m+4,CD=1﹣m,OC=﹣m,CP=1﹣4m﹣m2,
∴DP=1﹣4m﹣m2﹣1+m=﹣3m﹣m2.
在y=x﹣1中,当y=0时,x=1,∴(1,0),∴OF=1,
∴CF=1﹣m.AF=4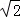 .∵PC⊥x轴,∴∠PCF=90°,
.∵PC⊥x轴,∴∠PCF=90°,
∴∠PCF=∠APD,∴CF∥AP,∴△APD∽△FCD,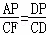 ,
,
∴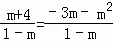 ,
,
解得:m=1舍去或m=﹣2,
∴P(﹣2,﹣5)
如图3,当∠PAD=90°时,作AE⊥x轴于E,
∴∠AEF=90°.CE=﹣3﹣m,EF=4,AF=4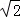 ,PD=1﹣m﹣(1﹣4m﹣m2)=3m+m2.
,PD=1﹣m﹣(1﹣4m﹣m2)=3m+m2.
∵PC⊥x轴,∴∠DCF=90°,∴∠DCF=∠AEF,∴AE∥CD.∴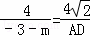 ,
,
∴AD=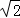 (﹣3﹣m).∵△PAD∽△FEA,∴
(﹣3﹣m).∵△PAD∽△FEA,∴ ,∴
,∴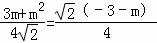 ,
,
∴m=﹣2或m=﹣3
∴P(﹣2,﹣5)或(﹣3,﹣4)与点A重合,舍去,
∴P(﹣2,﹣5).
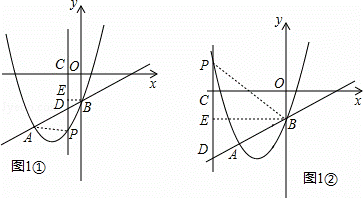

 阅读快车系列答案
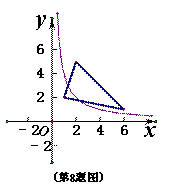
阅读快车系列答案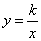 在第一象限内的图像与△ABC有交点,则
在第一象限内的图像与△ABC有交点,则 的取值范围是
的取值范围是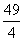 B.6≤
B.6≤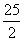
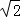 x+m=0,有两个不相等的实数根.
x+m=0,有两个不相等的实数根. ;
;