题目内容
15.计算:(1)(-$\frac{2{a}^{2}}{c}$)3÷$\frac{2a}{{c}^{2}}$•($\frac{c}{2a}$)2
(2)($\frac{x+1}{{x}^{2}-x}-\frac{x}{{x}^{2}-2x+1}$)÷$\frac{1}{x}$,其中x=$\sqrt{2}$+1.
分析 (1)直接根据分式混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原式=-$\frac{8{a}^{6}}{{c}^{3}}$•$\frac{{c}^{2}}{2a}$•$\frac{{c}^{2}}{4{a}^{2}}$
=-$\frac{4{a}^{5}}{c}$•$\frac{{c}^{2}}{4{a}^{2}}$
=a3c;
(2)原式=[$\frac{x+1}{x(x-1)}$-$\frac{x}{(x-1)^{2}}$]•x
=$\frac{(x+1)(x-1)-{x}^{2}}{{x(x-1)}^{2}}$•x
=$\frac{{x}^{2}-1-{x}^{2}}{{x(x-1)}^{2}}$•x
=$\frac{-1}{{x(x-1)}^{2}}$•x
=$\frac{-1}{{(x-1)}^{2}}$,
当x=$\sqrt{2}$+1时,原式=$\frac{-1}{{(\sqrt{2}+1-1)}^{2}}$=-$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
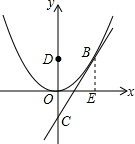 如图,直线y=kx-k2(k>0)与y轴交于C,与抛物线y=ax2有唯一公共点B,BE⊥x轴于E,D(0,4),若经过D、O、E三点的圆与抛物线的交点恰好为点B,求k的值.
如图,直线y=kx-k2(k>0)与y轴交于C,与抛物线y=ax2有唯一公共点B,BE⊥x轴于E,D(0,4),若经过D、O、E三点的圆与抛物线的交点恰好为点B,求k的值.