题目内容
 如图,已知:∠A=∠D=90°,AB=CD.
如图,已知:∠A=∠D=90°,AB=CD.求证:OB=OC.
考点:全等三角形的判定与性质
专题:证明题
分析:因为∠A=∠D=90°,AB=CD,BC=CB,知Rt△BAC≌Rt△CDB(HL),所以∠ACB=∠DBC,即∠OCB=∠OBC,所以有OB=OC.
解答:证明:∵∠A=∠D=90°,AB=CD,BC=CB,
在Rt△BAC与Rt△CDB中,
∴Rt△BAC≌Rt△CDB(HL).
∴∠ACB=∠DBC.
∴∠OCB=∠OBC.
∴OB=OC(等角对等边).
在Rt△BAC与Rt△CDB中,
|
∴Rt△BAC≌Rt△CDB(HL).
∴∠ACB=∠DBC.
∴∠OCB=∠OBC.
∴OB=OC(等角对等边).
点评:本题考查了直角三角形的判定和性质;由三角形全等得角相等,从而得到线段相等是证明题中常用的方法,注意掌握应用.

练习册系列答案
相关题目
用同样大小的黑色五角星按图所示的方式摆图案,按照这样的规律摆下去,第13个图案需要的黑色五角星的个数是( )


| A、18 | B、19 | C、21 | D、22 |
在平面直角坐标系中,将抛物线y=x2+1向右平移2个单位,再向下平移4个单位,得到的抛物线的解析式是( )
| A、y=(x+2)2-3 |
| B、y=(x-2)2-3 |
| C、y=(x-2)2+5 |
| D、y=(x+2)2+5 |
已知
=
,则
的值是( )
| b |
| a |
| 5 |
| 13 |
| a+b |
| a-b |
A、
| ||
B、
| ||
C、
| ||
D、
|
当地面高于海平面1米时,记作“+1米”,那么地面低于海平面10米时,记作( )
| A、-1米 | B、+1米 |
| C、-10米 | D、+10米 |
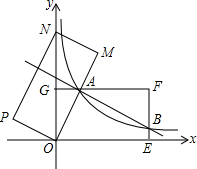 如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.
如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A. 如图,直线y=2x-2分别交x轴、y轴于B、A两点,交双曲线y=
如图,直线y=2x-2分别交x轴、y轴于B、A两点,交双曲线y=