题目内容
 如图,边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AEFG,则它们的公共部分面积等于( )
如图,边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AEFG,则它们的公共部分面积等于( )A、
| ||||
B、1-
| ||||
C、1-
| ||||
D、
|
考点:旋转的性质,正方形的性质
专题:
分析:设CD与EF的交点为H,连接AH,利用“HL”求出Rt△ADH和Rt△AEH全等,根据全等三角形对应角相等可得∠DAH=∠EAH,再求出∠DAH=30°,然后解直角三角形求出DH,再根据公共部分的面积=2S△ADH列式计算即可得解.
解答: 解:如图,设CD与EF的交点为H,连接AH,
解:如图,设CD与EF的交点为H,连接AH,
在Rt△ADH和Rt△AEH中,
,
∴Rt△ADH≌Rt△AEH(HL),
∴∠DAH=∠EAH,
∵旋转角∠BAE=30°,
∴∠DAH=
(90°-30°)=30°,
∵正方形ABCD的边长为1,
∴DH=1×
,
∴公共部分的面积=2S△ADH=2×
×1×
=
.
故选A.
 解:如图,设CD与EF的交点为H,连接AH,
解:如图,设CD与EF的交点为H,连接AH,在Rt△ADH和Rt△AEH中,
|
∴Rt△ADH≌Rt△AEH(HL),
∴∠DAH=∠EAH,
∵旋转角∠BAE=30°,
∴∠DAH=
| 1 |
| 2 |
∵正方形ABCD的边长为1,
∴DH=1×
| ||
| 3 |
∴公共部分的面积=2S△ADH=2×
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
故选A.
点评:本题考查了旋转的性质,正方形的性质,解直角三角形,作辅助线构造出全等三角形并求出三角形的锐角是30°是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
一个直角三角形两直角边长分别为3和4,下列说法正确的是( )
| A、斜边长为25 | ||
| B、三角形的周长为25 | ||
C、斜边长上的高为
| ||
| D、三角形的面积为20 |
下列各式正确的是( )
| A、cos60°<sin45°<tan45° |
| B、sin45°<cos60°<tan45° |
| C、sin45°<tan45°<cos60 |
| D、cos60°<tan45°<sin45° |
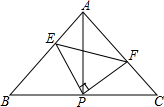 如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),给出以下五个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=
如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),给出以下五个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF= 如图,AB是⊙O的直径,C是BA延长线上一点,点D在☉O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=20°,则∠BOE的度数是
如图,AB是⊙O的直径,C是BA延长线上一点,点D在☉O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=20°,则∠BOE的度数是